- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-19 22:14.
- Modificat ultima dată 2025-01-23 12:43.
Scăderea înseamnă pur și simplu scăderea unui număr din altul. Este ușor să scădem un număr întreg din altul, dar scăderea poate fi dificilă dacă scădem fracții sau zecimale. După ce înțelegeți scăderea, veți putea folosi concepte matematice mai complexe și veți putea adăuga, înmulți și împărți numerele mai ușor.
Etapa
Metoda 1 din 6: Scăderea numerelor mari mari prin împrumut

Pasul 1. Notați un număr mare
De exemplu, doriți să rezolvați 32 - 17. Notați mai întâi 32.

Pasul 2. Scrieți numărul mai mic chiar sub el
Asigurați-vă că plasați valorile zecilor și cele în coloanele corecte, astfel încât 3 din 32 să fie direct peste 1 din 17 și 2 din 32 să fie direct peste 7 din 17.
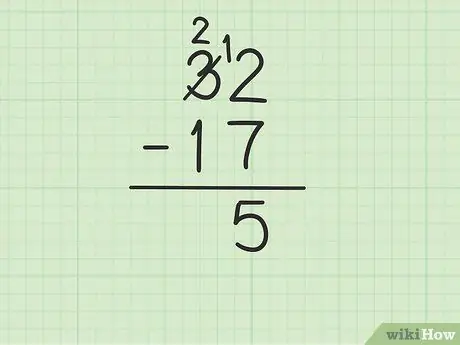
Pasul 3. Se scade numărul de sus din coloana unități din numărul din partea de jos
Cu toate acestea, acest lucru se poate complica dacă numărul de jos este mai mare decât numărul de sus. În acest caz, 7 este mai mare decât 2. Iată ce trebuie să faceți:
- Trebuie să împrumutați din numărul 3 din 32 (cunoscut și ca grupare), pentru a transforma 2 în 12.
- Treceți numărul 3 din 32 și înlocuiți-l cu numărul 2, în timp ce numărul 2 devine 12.
- Acum puteți scădea 12 - 7, care este egal cu 5. Scrieți 5 sub cele două numere pe care le scădeți, astfel încât acestea să se afle în coloana unităților noului rând.
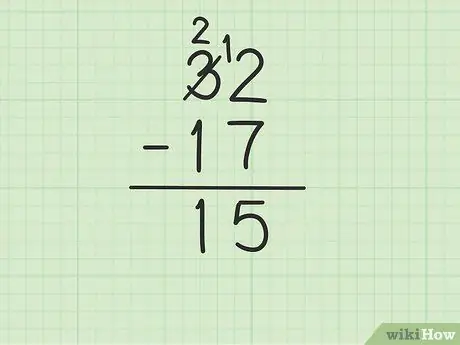
Pasul 4. Se scade numărul de sus din coloana zecilor din numărul de jos
Amintiți-vă că 3 a devenit 2. Acum scade 1 din 17 din 2 de mai sus pentru a obține (2-1) 1. Scrie 1 mai jos, în coloana zecilor, în stânga lui 5 în coloana unități. Scrii 15. Adică 32 - 17 = 15.
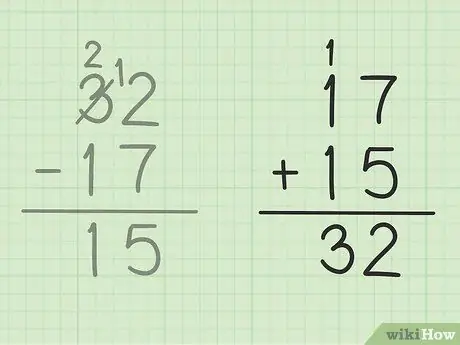
Pasul 5. Verifică-ți munca
Dacă doriți să vă asigurați că ați scăzut corect două numere, atunci tot ce trebuie să faceți este să adăugați răspunsul cu numărul mai mic pentru a face un număr mare. În această problemă, trebuie să adăugați răspunsul dvs., 15 la numărul mai mic de scădere, 17. 15 + 17 = 32, astfel încât răspunsul dvs. să fie corect. Sigur!
Metoda 2 din 6: Scădeți numere întregi mici
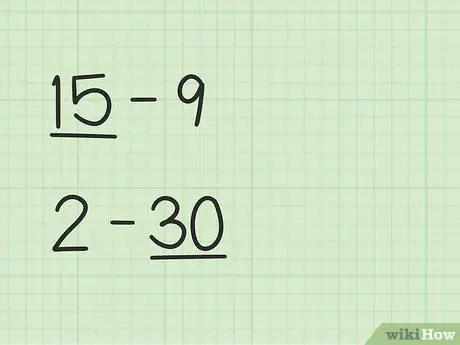
Pasul 1. Găsiți numărul mai mare
Probleme precum 15 -9 vor avea un mod diferit de 2-30.
- În întrebările 15 - 9, primul număr, 15, este mai mare decât al doilea număr, 9.
- În întrebările 2 - 30, al doilea număr, 30, este mai mare decât primul număr, 2.
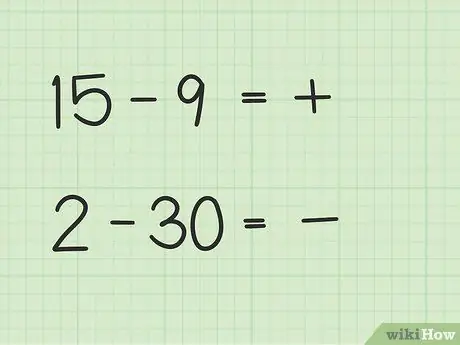
Pasul 2. Decideți dacă răspunsul dvs. va fi pozitiv sau negativ
Dacă primul număr este mai mare, răspunsul este pozitiv. Dacă al doilea număr este mai mare, răspunsul este negativ.
- În prima întrebare, 15 - 9, răspunsul dvs. este pozitiv, deoarece primul număr este mai mare decât al doilea număr.
- În a doua întrebare, 2 - 30, răspunsul dvs. este negativ, deoarece al doilea număr este mai mare decât primul număr.
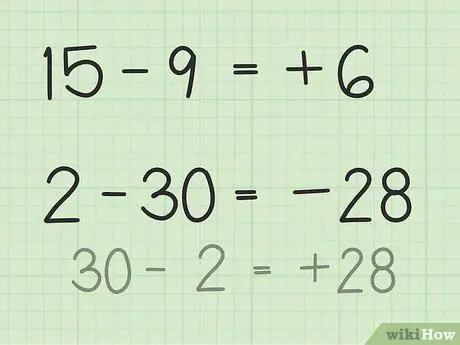
Pasul 3. Găsiți diferența dintre două numere
Pentru a scădea două numere, trebuie să vă imaginați diferența dintre cele două numere și să calculați numerele dintre ele.
- Pentru întrebările 15 - 9, imaginați-vă un teanc de 15 jetoane de poker. Aruncați 9 jetoane și doar 6. Deci, 15 - 9 = 6. Vă puteți imagina și o linie numerică. Gândiți-vă la numerele de la 1 la 15, apoi aruncați sau returnați 9 unități pentru a obține 6.
- Pentru întrebările 2 - 30, cel mai simplu mod de a rezolva acest lucru este de a inversa numărul și de a face rezultatul negativ după scăderea. Deci, 30 - 2 = 28 deci 28 și 30 au o diferență de 2. Acum, faceți rezultatul negativ pentru că ați stabilit deja că răspunsul este negativ deoarece al doilea număr este mai mare decât primul număr. Deci, 2 - 30 = -28.
Metoda 3 din 6: scăderea zecimalelor
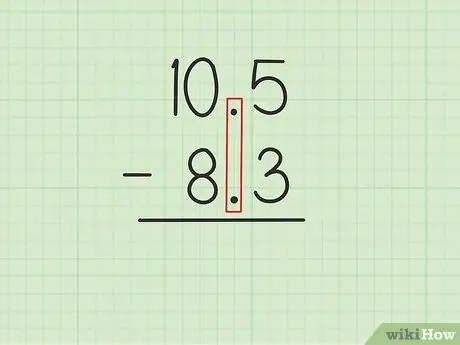
Pasul 1. Scrieți numărul mai mare peste numărul mai mic cu punctele zecimale aliniate
Să presupunem că doriți să rezolvați următoarele probleme: 10, 5 - 8, 3. Scrieți 10, 5 peste 8, 3 astfel încât punctele zecimale ale celor două numere să fie paralele., 5 din 10, 5 trebuie să fie direct deasupra, 3 din 8, 3 și 0 din 10, 5 trebuie să fie peste 8 din 8, 3.
Dacă aveți o problemă, deoarece cele două numere nu au același număr după punctul zecimal, scrieți 0 în gol până când suma numerelor este aceeași. De exemplu, problema este 5, 32 - 4, 2, o puteți scrie ca 5, 32 - 4, 2 0. Acest lucru nu va schimba valoarea celui de-al doilea număr, dar va facilita scăderea celor două numere.

Pasul 2. Se scade numărul de sus din coloana zecilor din numărul de mai jos
În acest caz, trebuie să scazi 3 din 5. 5 - 3 = 2, deci trebuie să scrii 2 sub 3 din 8, 3.
Asigurați-vă că ați pus un punct zecimal în răspuns, astfel încât să fie scris, 2

Pasul 3. Se scade numărul de deasupra coloanei unități din numărul de sub ea
Trebuie să scazi 8 din 0. Împrumută 1 din partea zecilor pentru a schimba 0 la 10 și scade 10 - 8 pentru a obține 2. De asemenea, poți număra 10 - 8 fără împrumut deoarece nu există numere în coloana a doua zeci. Scrieți răspunsul sub 8, în stânga punctului zecimal.

Pasul 4. Notați rezultatul final
Rezultatul dvs. final este 2, 2.

Pasul 5. Verifică-ți munca
Dacă doriți să vă asigurați că scăderea zecimală este corectă, tot ce trebuie să faceți este să adăugați răspunsul cu numărul mai mic pentru a face numărul mai mare. 2, 2 + 8, 3 = 10, 5, deci ați terminat.
Metoda 4 din 6: Scădeți fracțiile

Pasul 1. Aliniați numitorul și numărătorul fracției
Să presupunem că doriți să rezolvați problemele 13/10 - 3/5. Scrieți problema astfel încât cei doi numărători, 13 și 3 și cei doi numitori, 10 și 5 să fie unul față de celălalt. Aceste două numere sunt separate printr-un semn de scădere. Acest lucru vă va ajuta să vizualizați problema și să o rezolvați mai ușor.

Pasul 2. Găsiți cel mai puțin numitor comun
Numitorul cel mai puțin comun este cel mai mic număr care poate fi împărțit la două numere. În acest exemplu, trebuie să găsiți cel mai mic numitor comun care este divizibil cu 10 și 5. Veți descoperi că 10 este cel mai mic numitor comun pentru ambele numere, deoarece 10 este divizibil cu 10 și 5.
Rețineți că cel mai mic numitor comun al a două numere nu este întotdeauna unul dintre ele. De exemplu, cel mai mic numitor comun pentru 3 și 2 este 6 deoarece 6 este cel mai mic număr care poate fi împărțit la două numere
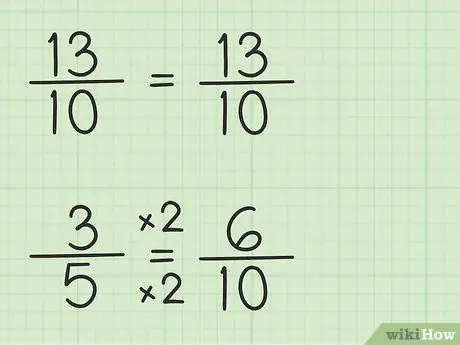
Pasul 3. Notați fracțiile folosind același numitor
Fracția 13/10 poate fi scrisă în același mod deoarece numitorul este 10, cel mai mic numitor comun, care este 10, ori 1. Cu toate acestea, fracția 3/5 trebuie rescrisă deoarece numitorul este 5, cel mai mic numitor comun, care este 10, ori 2. Deci fracția 3/5 trebuie înmulțită cu 2/2 pentru a face numitorul 10, deci 3/5 x 2/2 = 6/10. Ați găsit fracția echivalentă. 3/5 este echivalent cu 6/10, deși 6/10 vă permite să scădeți primul număr, 13/10.
Scrieți o nouă întrebare ca aceasta: 13/10 - 6/10
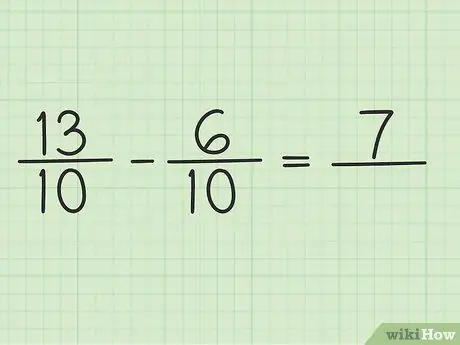
Pasul 4. Se scade numeratorul la două numere
Scade doar 13 - 6, deci rezultatul este 7. Nu poți schimba numitorul fracției.
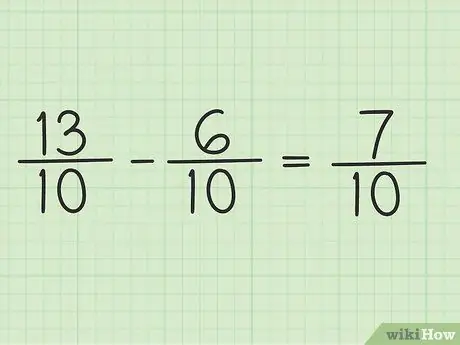
Pasul 5. Scrieți noul numărător peste același numitor pentru a obține rezultatul final
Noul numărător este 7. Ambele fracții au un numitor de 10. Rezultatul dvs. final este 7/10.
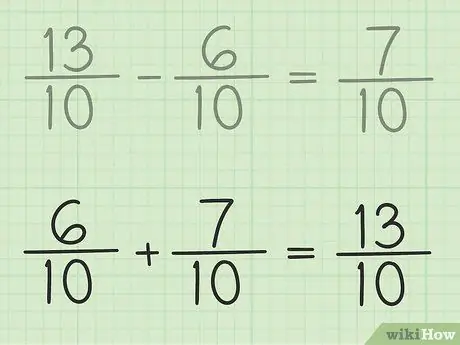
Pasul 6. Verifică-ți munca
Dacă doriți să vă asigurați că scadeți fracția corect, adăugați răspunsul și fracția mai mică, astfel încât rezultatul să fie o fracție mai mare. 7/10 + 6/10 = 13/10. S-a terminat.
Metoda 5 din 6: Scăderea fracțiilor din numerele întregi

Pasul 1. Notați problema
De exemplu, să presupunem că doriți să rezolvați următoarea problemă: 5 -. Scrie pe hartie.
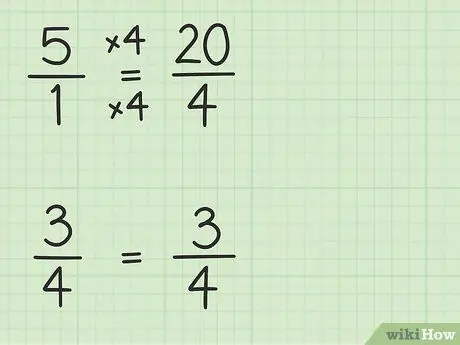
Pasul 2. Convertiți numerele întregi în fracții care au același numitor ca alte fracții
Veți converti 5 într-o fracție cu un numitor de 4 pentru a putea scădea două numere. Deci, trebuie să vă gândiți la 5 ca la o fracțiune de 5/1. Apoi, puteți înmulți numeratorul și numitorul noii fracții cu 4 pentru a face numitorii celor două numere la fel. Deci 5/1 x 4/4 = 20/4. Această fracție este egală cu 5, dar vă permite să scădeți două numere.
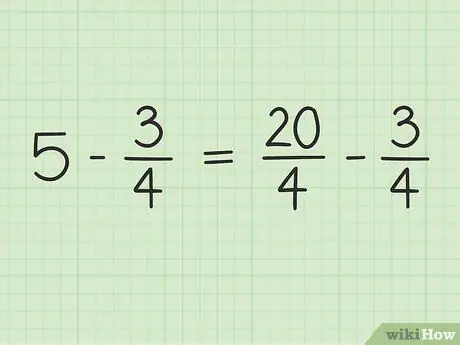
Pasul 3. Rescrie problema
Noua problemă poate fi scrisă astfel: 20/4 - 3/4.
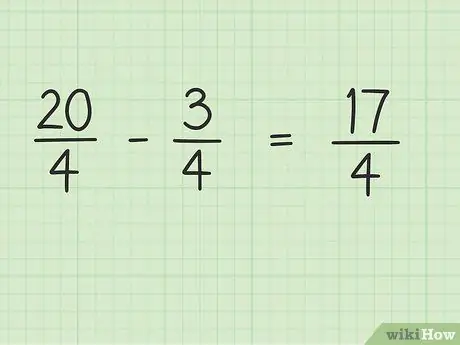
Pasul 4. Se scade numeratorul fracției, în timp ce numitorul rămâne același
Acum, scade doar 20 cu 3 pentru a obține rezultatul final. 20 - 3 = 17, deci 17 este noul numărător. Puteți lăsa același numitor.
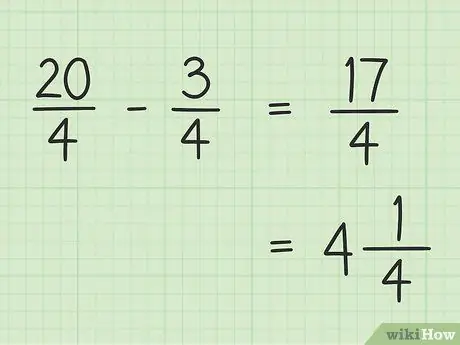
Pasul 5. Notează-ți rezultatul final
Rezultatul dvs. final este 17/4. Dacă doriți să-l scrieți ca număr mixt, împărțiți 17 la 4 astfel încât rezultatul să fie 4 și restul să fie 1, astfel încât 17/4 final să fie egal cu 4.
Metoda 6 din 6: scăderea variabilelor
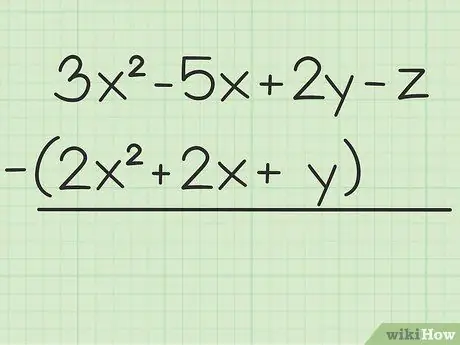
Pasul 1. Notați problema pe care doriți să o rezolvați
De exemplu următoarea întrebare: 3x2 - 5x + 2y - z - (2x2 + 2x + y). Scrieți primul set de variabile peste al doilea.
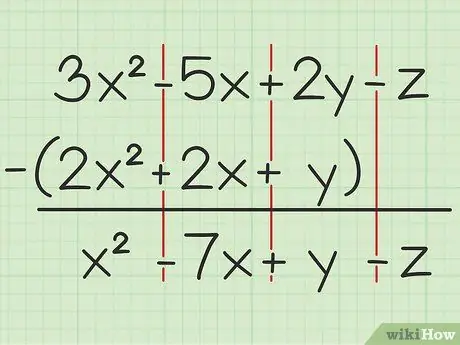
Pasul 2. Scădeți aceleași variabile
Dacă întâlniți o variabilă, puteți adăuga sau scădea doar aceeași variabilă și care este scrisă cu același grad de pătrat. Asta înseamnă că poți scădea 4x2 de la 7x2, dar nu poate scădea 4x din 4y. Deci, puteți descompune problema astfel:
- 3x2 - 2x2 = x2
- -5x - 2x = -7x
- 2y - y = y
- -z - 0 = -z
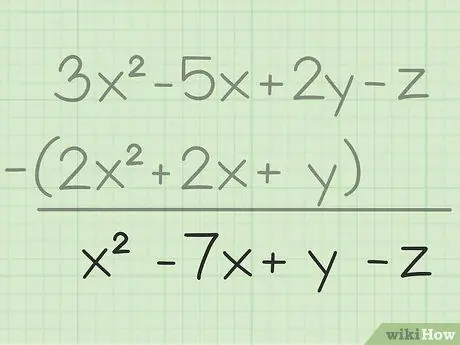
Pasul 3. Notați rezultatul final
Ați scăzut toate aceleași variabile, tot ce trebuie să faceți este să scrieți rezultatul final care va conține toate variabilele pe care le-ați scăzut. Iată rezultatul final:






