- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:22.
- Modificat ultima dată 2025-01-23 12:43.
Forța normală este magnitudinea forței necesare pentru a nega celelalte forțe în orice scenariu. Cel mai bun mod de a-l găsi depinde de starea obiectului și de variabilele pe care le aveți. Continuați să citiți pentru a afla mai multe.
Etapa
Metoda 1 din 5: Stil normal în repaus
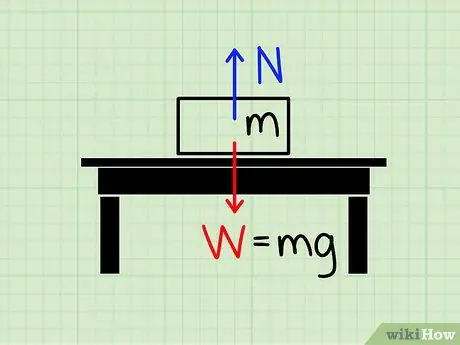
Pasul 1. Înțelegeți semnificația forței normale
Forța normală se referă la magnitudinea forței utilizate pentru a nega forța gravitațională.
Imaginați-vă un bloc în repaus pe o masă. Forța gravitațională trage blocul spre pământ, dar în mod clar, există o forță care acționează, împiedicând blocul să zdrobească masa și să cadă la pământ. Se numește forța care acționează pentru a opri acest bloc în ciuda forței gravitaționale stil normal.
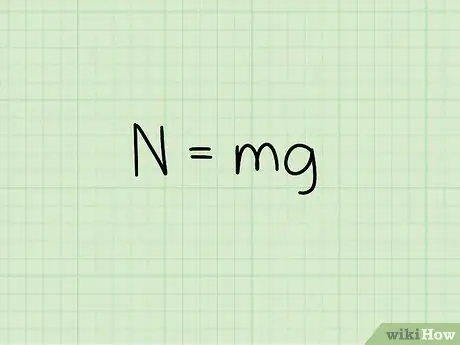
Pasul 2. Cunoașteți ecuația forței normale asupra unui obiect în repaus
Când calculați forța normală a unui obiect atunci când acesta este în repaus pe o suprafață plană, utilizați formula: N = m * g
- În această ecuație, N simbolizează stilul normal, m reprezintă masa obiectului și g reprezintă accelerația datorată gravitației.
- Pentru un obiect care se află în repaus pe o suprafață plană, fără să acționeze o forță externă, forța normală este egală cu greutatea obiectului. Pentru a menține un obiect în repaus, forța normală trebuie să fie egală cu forța gravitațională care acționează asupra obiectului. Forța gravitațională care acționează asupra unui obiect este greutatea obiectului sau masa obiectului de ori accelerarea datorată gravitației.
- Exemplu: Găsiți forța normală a unui bloc cu o masă de 4,2 kg.
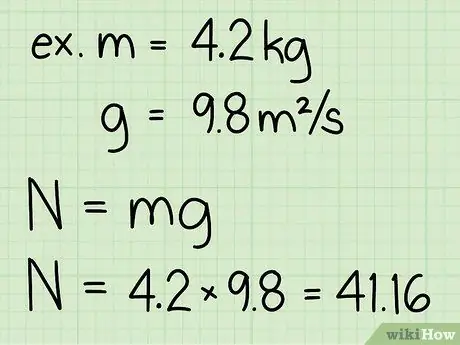
Pasul 3. Înmulțiți masa obiectului și accelerația datorată gravitației
Această multiplicare va produce greutatea obiectului, care, desigur, este egală cu forța normală a obiectului în repaus.
- Rețineți că accelerația datorată gravitației pe suprafața pământului este întotdeauna constantă: g = 9,8 m / s2
- Exemplu: greutate = m * g = 4, 2 * 9, 8 = 41, 16

Pasul 4. Notați-vă răspunsurile
Pasul anterior va rezolva problema, oferindu-vă răspunsul.
Exemplu: Forța normală este 41, 16 N
Metoda 2 din 5: Forța normală pe un plan înclinat
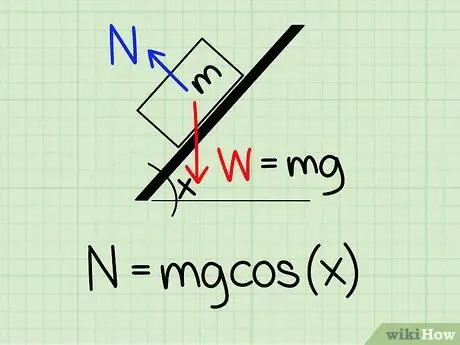
Pasul 1. Folosiți ecuația corectă
Pentru a calcula forța normală asupra unui obiect înclinat cu un anumit unghi, trebuie să utilizați formula: N = m * g * cos (x)
- Pentru această ecuație, N simbolizează stilul normal, m reprezintă masa obiectului g reprezintă accelerația datorată gravitației și X reprezintă unghiul oblic.
- Exemplu: Găsiți forța normală a unui bloc cu o masă de 4,2 kg, care se sprijină pe un plan înclinat cu o înclinare de 45 de grade.

Pasul 2. Găsiți cosinusul unghiului
Cosinusul unghiului este egal cu sinusul unghiului complementar sau latura adiacentă împărțită la hipotenuza triunghiului format de panta.
- Această valoare este adesea determinată cu un calculator, deoarece cosinusul oricărui unghi este întotdeauna constant, dar îl puteți calcula și manual.
- Exemplu: cos (45) = 0,71
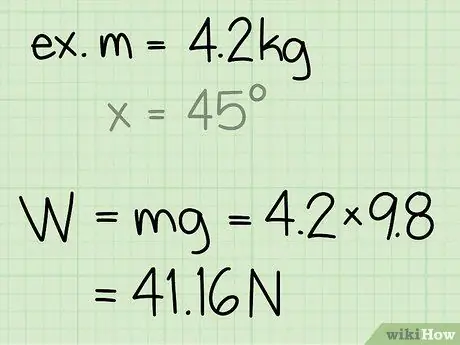
Pasul 3. Găsiți greutatea obiectului
Greutatea unui obiect este egală cu masa obiectului de ori accelerarea datorată gravitației.
- Rețineți că accelerația datorată gravitației pe suprafața pământului este întotdeauna constantă: g = 9,8 m / s2
- Exemplu: greutate = m * g = 4, 2 * 9, 8 = 41, 16
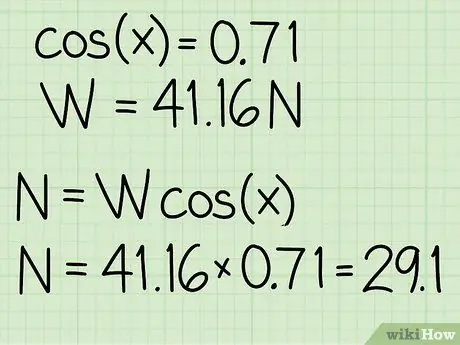
Pasul 4. Înmulțiți cele două valori
Pentru a găsi forța normală, trebuie să înmulțiți greutatea obiectului cu cosinusul unghiului de înclinare.
Exemplu: N = m * g * cos (x) = 41, 16 * 0, 71 = 29, 1
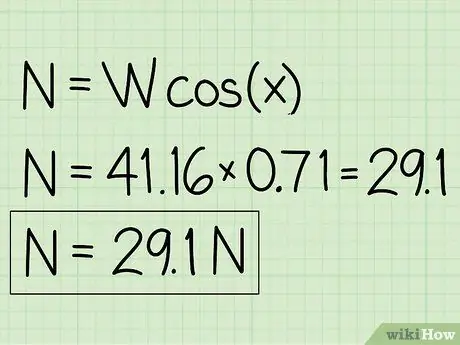
Pasul 5. Notați-vă răspunsurile
Pasul anterior va rezolva problema și vă va oferi răspunsul.
- Rețineți că atunci când un obiect este odihnit pe o înclinație, forța normală va fi mai mică decât greutatea obiectului.
- Exemplu: Forța normală este 29,1 N.
Metoda 3 din 5: Stil normal cu stil exterior în jos
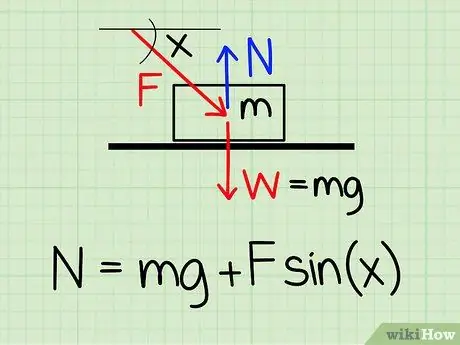
Pasul 1. Folosiți ecuația corectă
Pentru a calcula forța normală asupra unui obiect în repaus dacă există o forță externă descendentă asupra obiectului, utilizați ecuația: N = m * g + F * sin (x) '
- N simbolizează stilul normal, m reprezintă masa obiectului g reprezintă accelerația datorată gravitației, F simbolizează stilul extern și X reprezintă unghiul dintre obiect și direcția forței externe.
- Exemplu: Găsiți forța normală a unui obiect cu o masă de 4,2 kg dacă obiectul este împins de o persoană la un unghi de 30 de grade și o forță de 20,9 N.
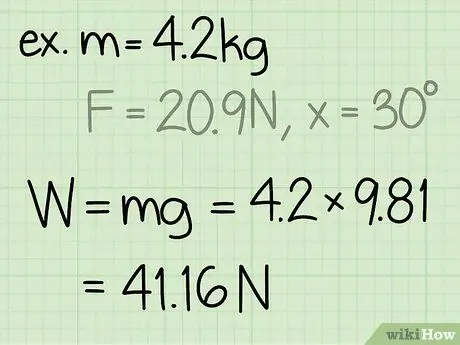
Pasul 2. Găsiți greutatea obiectului
Greutatea unui obiect este egală cu masa obiectului de ori accelerarea datorată gravitației.
- Rețineți că accelerația datorată gravitației pe suprafața pământului este întotdeauna constantă: g = 9,8 m / s2
- Exemplu: greutate = m * g = 4, 2 * 9, 8 = 41, 16
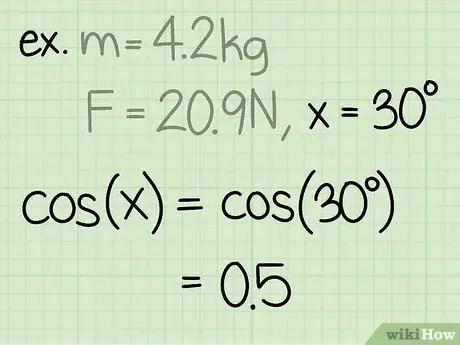
Pasul 3. Găsiți sinusul unghiului
Sinusul unui unghi se calculează prin împărțirea laturii triunghiului opus unghiului, la hipotenuza unghiului.
Exemplu: sin (30) = 0,5

Pasul 4. Înmulțiți sinusul cu forța externă
Forța externă, în acest exemplu, se referă la forța descendentă care lovește obiectul.
Exemplu: 0, 5 * 20, 9 = 10, 45
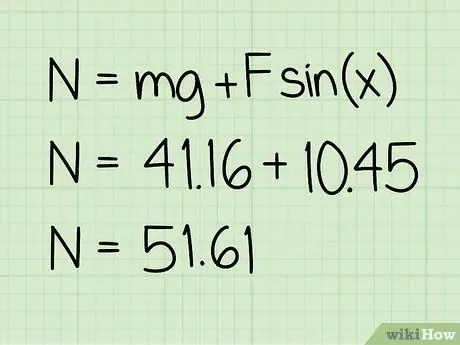
Pasul 5. Adăugați această valoare la greutate
Această sumă va da magnitudinea forței normale care acționează.
Exemplu: 10, 45 + 41, 16 = 51, 61
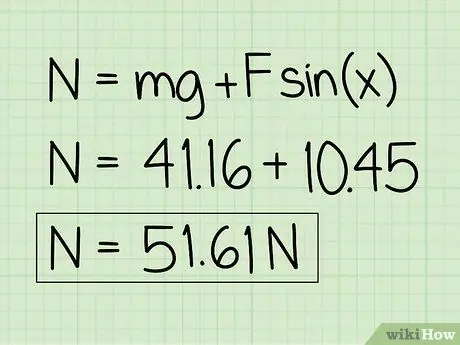
Pasul 6. Notați-vă răspunsurile
Rețineți că pentru un obiect în repaus care este afectat de o forță externă descendentă, forța normală va fi mai mare decât greutatea obiectului.
Exemplu: Forța normală este 51,61 N
Metoda 4 din 5: Stil normal cu Stil exterior în sus
Pasul 1. Folosiți ecuația corectă
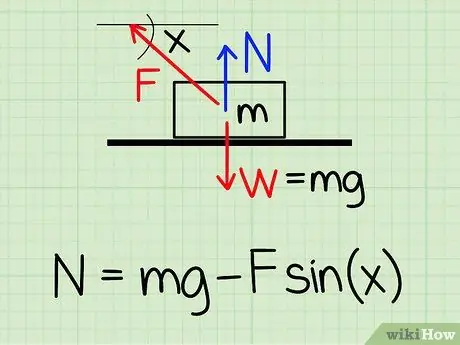
Pentru a calcula forța normală asupra unui obiect în repaus dacă există o forță externă ascendentă asupra obiectului, utilizați ecuația: N = m * g - F * sin (x) '
- N simbolizează stilul normal, m reprezintă masa obiectului g reprezintă accelerația datorată gravitației, F simbolizează stilul extern și X reprezintă unghiul dintre obiect și direcția forței externe.
- Exemplu: Găsiți forța normală a unui bloc cu o masă de 4,2 kg, dacă cineva trage blocul în sus la un unghi de 50 de grade și o forță de 20,9 N.

Pasul 2. Găsiți greutatea obiectului
Greutatea unui obiect este egală cu masa obiectului de ori accelerarea datorată gravitației.
- Rețineți că accelerația datorată gravitației pe suprafața pământului este întotdeauna constantă: g = 9,8 m / s2
- Exemplu: greutate = m * g = 4, 2 * 9, 8 = 41, 16
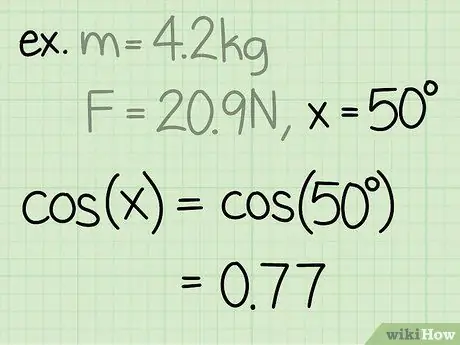
Pasul 3. Găsiți sinusul unghiului
Sinusul unui unghi se calculează prin împărțirea laturii triunghiului opus unghiului, la hipotenuza unghiului.
Exemplu: sin (50) = 0, 77

Pasul 4. Înmulțiți sinusul cu forța externă
Forța externă se referă la forța ascendentă care lovește obiectul, în acest caz.
Exemplu: 0,77 * 20, 9 = 16, 01
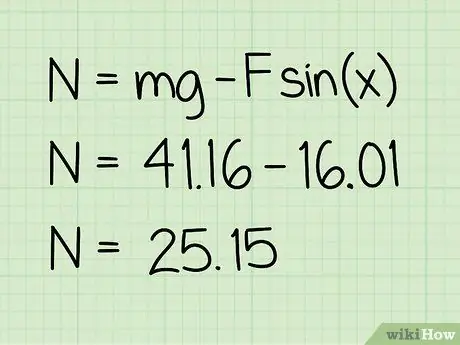
Pasul 5. Se scade această valoare din greutate
Scăderea pe care o faceți vă va oferi magnitudinea forței normale care acționează asupra ei.
Exemplu: 41, 16 - 16, 01 = 25, 15
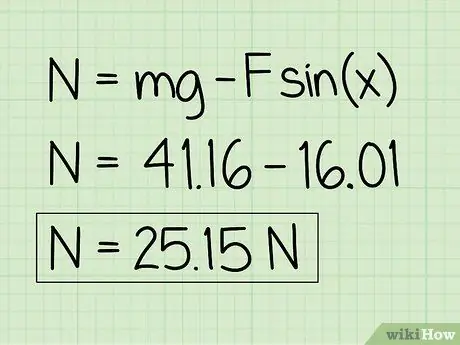
Pasul 6. Notați-vă răspunsurile
Rețineți că un obiect în repaus este afectat de o forță externă ascendentă, forța normală va fi mai mică decât greutatea obiectului.
Exemplu: Forța normală este de 25, 15 N
Metoda 5 din 5: Forță normală și frecare

Pasul 1. Cunoașteți ecuația de bază pentru frecare cinetică
Fricțiunea cinetică sau fricția unui obiect în mișcare este egală cu coeficientul de frecare de ori forța normală a unui obiect. În formă de ecuație: f = * N
- În această ecuație, f simbolizează fricțiunea, ️ reprezintă coeficientul de frecare și N reprezintă forța normală a obiectului.
- „Coeficientul de frecare” este raportul dintre forța de frecare și forța normală, care comprimă două suprafețe opuse.
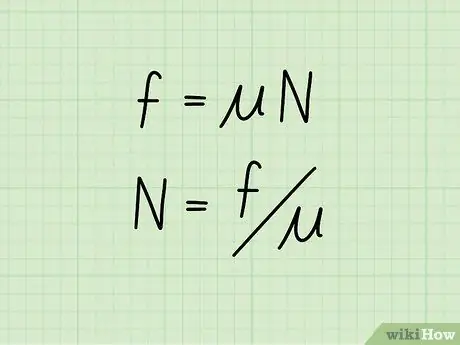
Pasul 2. Configurați ecuația pentru a izola forța normală
Dacă cunoașteți valoarea fricțiunii cinetice a unui obiect, precum și coeficientul său de frecare, puteți calcula forța normală folosind formula: N = f /
- Ambele părți ale ecuației inițiale sunt împărțite la ️, izolând astfel forța normală pe o parte în timp ce se calculează coeficientul de frecare și fricțiunea cinetică pe de altă parte.
- Exemplu: Găsiți forța normală a unui bloc dacă coeficientul de frecare este 0,4 și magnitudinea fricțiunii cinetice este de 40 N.
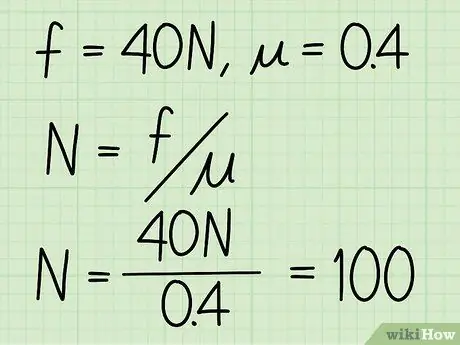
Pasul 3. Împarte fricțiunea cinetică la coeficientul de frecare
Practic, acesta este tot ce trebuie să faceți pentru a găsi magnitudinea forței normale.
Exemplu: N = f / = 40/0, 4 = 100
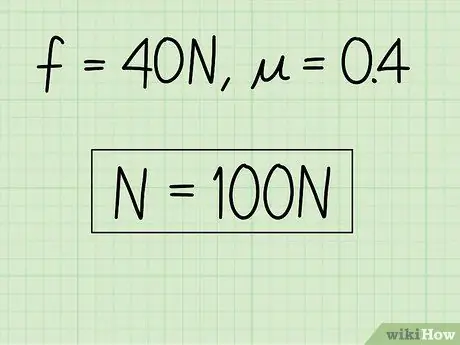
Pasul 4. Notați-vă răspunsurile
Dacă doriți, puteți verifica răspunsul conectându-l din nou la ecuația originală pentru frecare cinetică. Dacă nu doriți, ați rezolvat problema.






