- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-19 22:14.
- Modificat ultima dată 2025-01-23 12:43.
Matematica este grea. Este ușor să uitați chiar și conceptele de bază atunci când încercați să vă amintiți numeroasele principii și metode diferite. Iată două moduri noi de simplificare a fracțiilor.
Etapa
Metoda 1 din 4: Folosirea celui mai mare factor comun

Pasul 1. Notați factorii numărătorului și numitorului
Factorii sunt numere pe care le puteți înmulți pentru a obține un alt număr. De exemplu, 3 și 4 sunt factori de 12 deoarece îi puteți înmulți împreună pentru a obține 12. Pentru a nota factorii unui număr, trebuie doar să notați toate numerele care pot fi înmulțite pentru a obține acel număr și sunt divizibile de factori.
-
Notați factorii numărului de la cel mai mic la cel mai mare, fără a uita să includeți factorul 1. De exemplu, iată cum scrieți numărătorul și numitorul fracției 24/32:
- 24: 1, 2, 3, 4, 6, 8, 12, 24.
- 32: 1, 2, 4, 8, 16, 32.

Pasul 2. Găsiți cel mai mare factor comun (MCD) al numărătorului și numitorului
GCF este cel mai mare număr care poate împărți în mod egal două sau mai multe numere. După ce ați notat toți factorii numărului, tot ce trebuie să faceți este să găsiți cel mai mare număr care este același în ambele liste de factori.
-
24: 1, 2, 3, 4, 6,
Pasul 8., 12, 24.
-
32: 1, 2, 4,
Pasul 8., 16, 32.
-
MCD de 24 și 32 este 8, deoarece 8 este cel mai mare număr care poate împărți în mod egal 24 și 32.

Pasul 3. Împarte numeratorul și fracția la MCD
Acum, că aveți GCF, tot ce trebuie să faceți este să împărțiți numărătorul și numitorul la acel număr pentru a vă simplifica fracția la cea mai simplă formă. Iată cum să o faceți:
- 24/8 = 3
- 32/8 = 4
- Fracția simplă este 3/4.

Pasul 4. Verifică-ți munca
Dacă doriți să vă asigurați că ați simplificat fracția corect, trebuie doar să multiplicați noul numărător și numitorul cu GCF-ul lor pentru a recupera fracția originală. Iată cum să o faceți:
- 3 * 8 = 24
- 4 * 8 = 32
-
Ați revenit la forma sa originală, care este 24/32.
De asemenea, puteți verifica fracția pentru a vă asigura că nu poate fi simplificată în continuare. Deoarece 3 este un număr prim, acesta poate fi împărțit doar la 1 și el însuși, iar patru nu este divizibil cu 3, deci fracția nu poate fi simplificată în continuare
Metoda 2 din 4: Continuați să împărțiți prin numere mici

Pasul 1. Alegeți un număr mic
Folosind această metodă, trebuie să alegeți doar un număr mic, cum ar fi 2, 3, 4, 5 sau 7, pentru a începe. Uită-te la fracții pentru a te asigura că fiecare parte este divizibilă cu numărul pe care l-ai ales. De exemplu, dacă aveți o fracțiune 24/108, nu alegeți 5 deoarece nu sunt divizibile cu 5. Cu toate acestea, dacă aveți o fracțiune 25/60, 5 este numărul potrivit de utilizat.
Pentru fracțiunea 24/32, 2 este un număr bun. Deoarece ambele numere sunt numere pare, ele sunt divizibile cu 2

Pasul 2. Împarte numeratorul și numitorul fracției la număr
Noua fracție va consta dintr-un nou numărător și numitor, pe care îl obțineți după ce ați împărțit partea superioară și inferioară a fracției 24/32 la 2. Iată cum să o faceți:
- 24/2 = 12
- 32/2 = 16
- Noua dvs. fracție este 12/16.
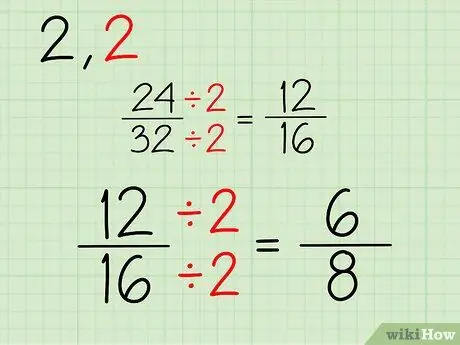
Pasul 3. Repetați
Continuați acest proces. Deoarece ambele numere sunt numere pare, puteți continua să împărțiți la 2. Dacă unul sau ambii dintre numeratori și numitori sunt numere impare, atunci puteți încerca să împărțiți cu un alt număr. Iată procesul de simplificare a fracției 12/16:
- 12/2 = 6
- 16/2 = 8
- Noua dvs. fracție este 6/8.

Pasul 4. Continuați să împărțiți numărul până când nu mai este divizibil
Noul numărător și numitorul sunt, de asemenea, numere pare, deci puteți continua să împărțiți la 2. Iată cum să faceți acest lucru:
- 6/2 = 3
- 8/2 = 4
- Noua dvs. fracție este 3/4.

Pasul 5. Asigurați-vă că fracția nu mai poate fi simplificată
În fracția 3/4, 3 este un număr prim, deci factorii sunt doar 1 și el însuși, iar 4 nu este divizibil cu 3, deci fracția nu mai poate fi simplificată. Dacă numărătorul sau numitorul fracției nu mai poate fi împărțit la numărul selectat, este posibil să îl puteți împărți cu un alt număr.
De exemplu, dacă aveți fracția 10/40 și împărțiți numărătorul și numitorul la 5, rezultatul este 2/8. Nu puteți continua să împărțiți numărătorul și fracția la 5, dar puteți împărți ambele la 2, astfel încât rezultatul final este 1/4

Pasul 6. Verifică-ți munca
Înmulțiți din nou 3/4 cu 2/2 de trei ori, pentru a vă asigura că obțineți fracția inițială, care este 24/32. Iată cum să o faceți:
- 3/4 * 2/2 = 6/8
- 6/8 * 2/2 = 12/16
- 12/16 * 2/2 = 24/32.
- Observați că împărțiți 24/32 la 2 * 2 * 2, care este același lucru cu împărțirea la 8, cel mai mare PIB de 24 și 32.
Metoda 3 din 4: Scrierea factorilor

Pasul 1. Notați fracția
Lăsați un spațiu mare pe partea dreaptă a hârtiei - veți avea nevoie de acesta pentru a nota factorii.

Pasul 2. Notați factorii numărătorului și numitorului
Singurii factori ai celor doi. Cea mai ușoară cale este ca factorii să se scrie unul peste celălalt. Începeți cu numărul 1 și notați factorii.
-
De exemplu, dacă fracția dvs. este 24/60, începeți cu 24.
Notați: 24 - 1, 2, 3, 4, 6, 8, 12, 24
-
Apoi, numărul 60.
Notați: 60 - 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60

Pasul 3. Găsiți și împărțiți la cel mai mare factor comun
Acest termen poate fi scris ca GCF în cartea dvs. tipărită. Care este cel mai mare număr care poate împărți numărătorul și numitorul? Oricare ar fi numărul, împărțiți ambele numere la numărul respectiv.
Pentru exemplul nostru, cel mai mare număr care este un factor al ambelor numere este 12. Astfel, împărțim 24 la 12 și 60 la 12, oferindu-ne 2/5 - fracția noastră simplă
Metoda 4 din 4: Folosirea unui arbore pentru factorii primi

Pasul 1. Găsiți factorii primi ai numărătorului și numitorului
Un număr prim este un număr care nu poate fi împărțit cu niciun alt număr (altul decât el însuși și 1, desigur). 2, 3, 5, 7 și 11 sunt exemple de numere prime.
- Începeți cu numeratorul. De la 24, împărțiți în 2 și 12. Deoarece 2 este deja un număr prim, nu mai trebuie să îl împărțiți! Apoi împărțiți 12 în 2 numere: 2 și 6. 2 sunt numere prime - minunat! Acum împarte 6 în 2 numere: 2 și 3. Acum ai 2, 2, 2 și 3 ca numere prime.
- Acum lucrați la numitor. De la 60, împărțiți arborele în 2 și 30. 30 apoi împărțiți în 2 și 15. Apoi împărțiți 15 în 3 și 5, ambele fiind numere prime. Acum aveți 2, 2, 3 și 5 ca numere prime.
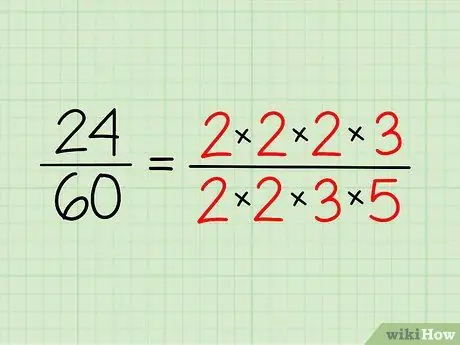
Pasul 2. Notați factorizarea primă a fiecărui număr
Notează numerele prime pe care le ai pentru fiecare număr și scrie-le sub formă de înmulțire. Nu trebuie să-l înmulțiți - este doar o modalitate de a face mai ușor de văzut.
- Deci, pentru 24, aveți 2 x 2 x 2 x 3 = 24.
- Pentru 60, aveți 2 x 2 x 3 x 5 = 60

Pasul 3. Eliminați aceiași factori
Orice număr care face parte din ambele numere poate fi aruncat. În acest exemplu, factorii egali sunt o pereche de 2 și unul 3. La revedere!
- Restul sunt 2 și 5 - sau 2/5! Același răspuns l-am obținut mai sus.
- Dacă numeratorul și numitorul fracției sunt numere pare, nu împărțiți doar la două. Continuați să faceți împărțirea până când numărul obținut nu poate fi împărțit din nou.






