- Autor Jason Gerald [email protected].
- Public 2024-01-15 08:22.
- Modificat ultima dată 2025-01-23 12:43.
Împărțirea unei fracții cu o fracție poate părea confuză la început, dar este de fapt foarte ușor. Tot ce trebuie să faceți este să răsturnați, să multiplicați și să simplificați! Acest articol vă va ghida prin proces și vă va arăta cât de ușor este să împărțiți o fracție cu o fracție.
Etapa
Partea 1 din 2: Înțelegerea modului de împărțire a fracțiilor la fracții
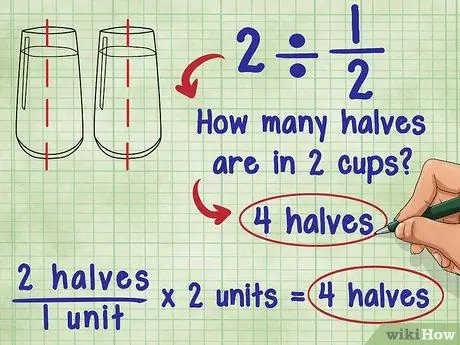
Pasul 1. Gândește-te la ce înseamnă împărțirea la o fracție
Despre 2 ÷ 1/2 a întrebat-o Ada: "Câte jumătăți sunt în 2?" Răspunsul este 4, deoarece fiecare unitate (1) este formată din două „jumătăți” și există 2 unități totale: 2 „jumătate” / 1 unitate * 2 unități = 4 „jumătate”.
- Încercați să vă imaginați aceeași ecuație folosind un pahar cu apă: Câte pahare și jumătate de apă sunt în 2 pahare de apă? Puteți turna 2 căni și jumătate de apă în fiecare pahar de apă. Asta înseamnă că, practic, adăugați „jumătate” pahare de apă și aveți două pahare: 2 „jumătate” / 1 cană * 2 cani = 4 „jumătate”.
- Aceasta înseamnă că, dacă fracția pe care o împărțiți este între 0 și 1, răspunsul este întotdeauna mai mare decât numărul inițial! Acest lucru este adevărat atunci când împărțiți un număr întreg sau o fracție la o fracție.

Pasul 2. Înțelegeți că împărțirea este opusul înmulțirii
Astfel, împărțirea la o fracție poate fi rezolvată prin înmulțirea cu reciprocul fracției. Reciprocitatea unei fracții (numită și „inversarea multiplicării”) este fracția inversată, astfel încât numeratorul și numitorul să schimbe locurile. Într-un moment, vom împărți fracțiile cu fracțiile, găsind reciprocul celei de-a doua fracții și înmulțind ambele fracții. Cu toate acestea, să ne uităm mai întâi la unele opuse:
- Reciprocitatea 3/4 este 4/3.
- Opusul 7/5 este 5/7.
- Reciprocitatea 1/2 este 2/1 sau 2.
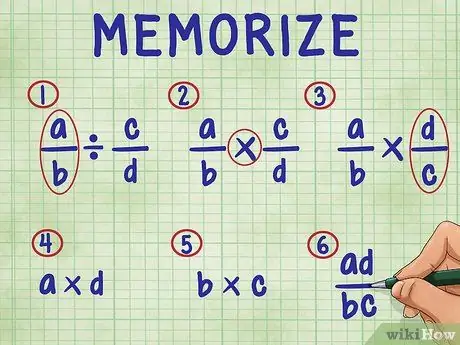
Pasul 3. Amintiți-vă pașii următori pentru a împărți o fracție la o fracție
În ordine, pașii includ:
- Lăsați prima fracție în ecuație.
- Schimbați semnul diviziunii cu semnul înmulțirii.
- Inversați a doua fracție (găsiți-o reciprocă).
- Înmulțiți numărătorul (numărul de sus) al ambelor fracții. Rezultatul multiplicării este numărătorul (partea de sus) a răspunsului dvs.
- Înmulțiți numitorul (numărul de jos) al ambelor fracții. Produsul produsului este numitorul răspunsului dvs.
- Simplificați-vă fracțiile simplificându-le la termenii lor cei mai simpli.
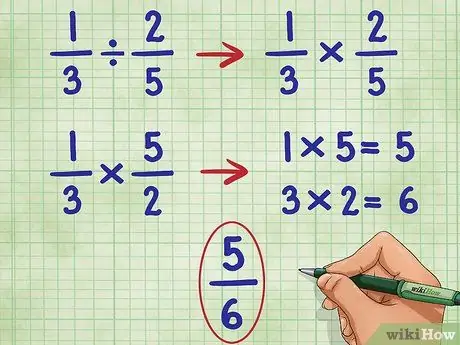
Pasul 4. Efectuați acești pași pentru exemplul 1/3 2/5
Vom începe prin a lăsa prima fracție și a converti semnul diviziunii în semnul înmulțirii:
- 1/3 ÷ 2/5 = Devine:
- 1/3 * _ =
- Acum, inversăm a doua fracție (2/5) pentru a-i găsi reciproc, care este 5/2:
- 1/3 * 5/2 =
- Acum, înmulțiți numărătorul (numărul de sus) al ambelor fracții, 1 * 5 = 5.
- 1/3 * 5/2 = 5/
- Acum, înmulțiți numitorul (numărul de jos) al ambelor fracții, 3 * 2 = 6.
- Acum avem: 1/3 * 5/2 = 5/6
- Această fracțiune nu poate fi simplificată, așa că avem răspunsul nostru.

Pasul 5. Încercați să vă amintiți următoarele rime pentru a vă ajuta să vă amintiți:
"Împărțirea fracțiilor este ușoară, inversați a doua fracție, apoi înmulțiți-vă. Nu uitați să simplificați, înainte de a fi timpul să mâncați."
Un alt ajutor util pentru memento vă spune ce să faceți cu fiecare parte a ecuației: „Lasă-mă (prima fracție), schimbă-mă (semnul diviziunii), inversează-mă (a doua fracție)”
Partea 2 din 2: Împărțirea fracțiilor la fracțiuni în probleme
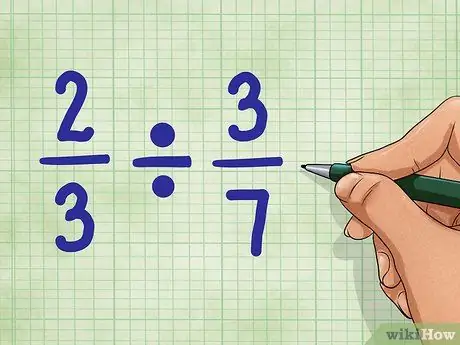
Pasul 1. Începeți cu exemple de întrebări
Să folosim 2/3 ÷ 3/7. Această întrebare cere numărul de părți egal cu 3/7, care poate fi găsit în valoarea 2/3. Nu-ți face griji. Nu este atât de dificil pe cât pare!
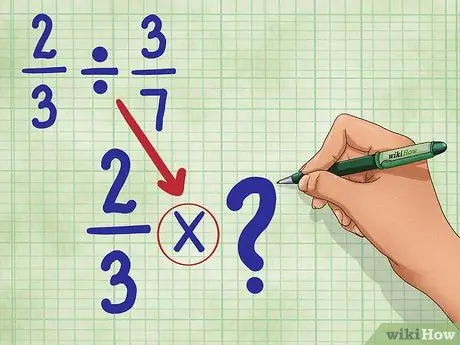
Pasul 2. Convertiți semnul diviziunii în semnul multiplicării
Noua dvs. ecuație va fi: 2/3 * _ (Vom umple acest gol într-o clipă.)
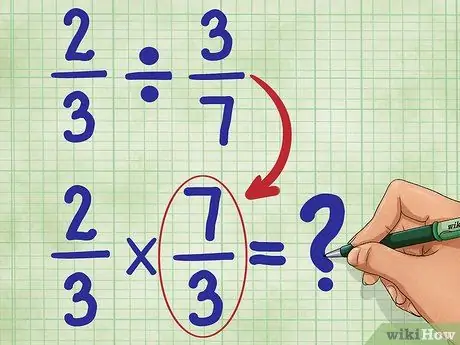
Pasul 3. Acum, găsiți reciprocul celei de-a doua fracții
Aceasta înseamnă răsturnarea 3/7, astfel încât numărătorul (3) să fie acum în partea de jos, iar numitorul (7) să fie acum în partea de sus. Reciprocitatea 3/7 este 7/3. Acum, scrieți noua dvs. ecuație:
2/3 * 7/3 = _

Pasul 4. Înmulțiți-vă fracțiile
În primul rând, înmulțiți numeratorii ambelor fracții: 2 * 7 = 14. 14 este numărătorul (numărul de sus) al răspunsului dvs. Apoi, înmulțiți numitorii ambelor fracții: 3 * 3 = 9. 9 este numitorul (numărul de jos) al răspunsului dvs. Acum, știi asta 2/3 * 7/3 = 14/9.
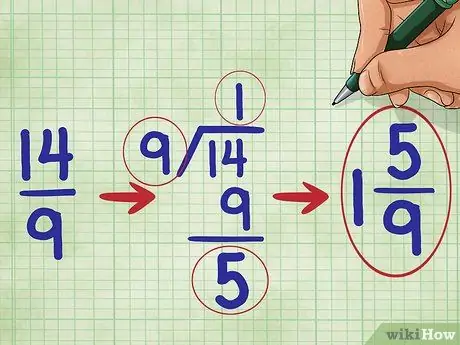
Pasul 5. Simplificați fracția
În această problemă, deoarece numeratorul fracției este mai mare decât numitorul, știm că fracția noastră este mai mare decât 1. Trebuie să o convertim într-un număr mixt. (Un număr mixt este un număr întreg și o fracție combinată, de exemplu 1 2/3.))
-
Mai întâi, împărțiți numeratorul
Pasul 14. cu 9.
Numărul 14 împărțit la 9 este egal cu unul cu restul de 5, deci ar trebui să notați fracția simplificată ca: 1 5/9 („Un cinci-nouăzeci”).
- Oprește-te, ai găsit răspunsul! Puteți specifica că nu mai puteți simplifica fracția, deoarece numitorul nu este divizibil cu numărătorul (9 nu este divizibil cu 5), iar numărătorul este un număr prim sau un număr întreg care este divizibil doar cu unul și cu numărul în sine.
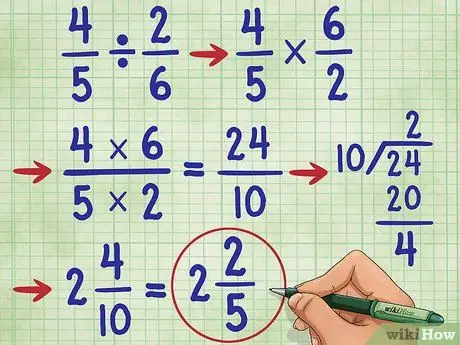
Pasul 6. Încercați un alt exemplu
Să încercăm întrebarea 4/5 ÷ 2/6 =. Mai întâi, schimbați semnul diviziunii cu semnul multiplicării (4/5 * _ =), apoi găsiți reciprocul 2/6, care este 6/2. Acum, aveți ecuația: 4/5 * 6/2 =_. Acum, înmulțiți numeratorul, 4 * 6 = 24, și numitorul 5* 2 = 10. Acum ai 4/5 * 6/2 = 24/10.
Acum, simplificați fracția. Deoarece numeratorul este mai mare decât numitorul, trebuie să convertim această fracție într-un număr mixt.
- Mai întâi, împărțiți numărătorul la numitor, (24/10 = 2 rămase 4).
- Scrie răspunsul ca 2 4/10. Încă putem simplifica din nou această fracțiune!
- Rețineți că 4 și 10 sunt numere pare. Deci, primul pas pentru simplificare este împărțirea fiecărui număr la 2. Obținem 2/5.
- Deoarece numitorul (5) nu este divizibil cu numărătorul (2) și 5 este un număr prim, știm că această fracție nu poate fi simplificată în continuare. Deci, răspunsul nostru este: 2 2/5.

Pasul 7. Obțineți ajutor suplimentar pentru simplificarea fracțiilor
Probabil ați petrecut mult timp învățând cum să simplificați fracțiile înainte de a încerca să le împărțiți una cu cealaltă. Cu toate acestea, dacă aveți nevoie de o reîmprospătare sau de alt ajutor, există câteva articole online grozave care vă pot fi de mare ajutor.
Articole legate de wikiHow
- Conversia fracțiilor comune în zecimale
- Calculul ariei unui cerc
- Împărțirea polinoamelor folosind diviziunea sintetică
- Împărțirea fracțiilor mixte






