- Autor Jason Gerald [email protected].
- Public 2023-12-16 11:34.
- Modificat ultima dată 2025-01-23 12:43.
Sistemul numeric zecimal (baza zece) are zece valori posibile (0, 1, 2, 3, 4, 5, 6, 7, 8 sau 9) pentru fiecare poziție numerică. În schimb, sistemul numeric binar (baza doi) are doar două valori posibile reprezentate cu 0 și 1 pentru fiecare poziție numerică. Deoarece sistemul de numere binare este limbajul intern al calculatoarelor electronice, programatorii serioși de calculatoare știu cum să convertească de la sistemul zecimal în sistem de numere binare. Urmați acești pași simpli și, de asemenea, cum să stăpâniți această conversie.
Etapa
Metoda 1 din 2: Împărțirea scurtă cu două cu restul

Pasul 1. Determinați problema
Pentru acest exemplu, să convertim numărul zecimal 15610 fie un număr binar. Scrieți numărul zecimal ca număr care trebuie împărțit în simbolul diviziunii inversate. Scrieți baza sistemului de numere de destinație (în acest exemplu „2” pentru binar) ca divizor în afara curbei simbolului diviziunii.
- Această metodă este mult mai ușor de înțeles când este desenată pe hârtie și mult mai ușoară pentru începători, deoarece se împarte doar la două.
- Pentru a evita confuzia înainte și după conversie, scrieți numărul de bază al sistemului numeric pe care îl calculați ca un indice (minuscule scrise cu litere normale ca semn distinctiv) pentru fiecare număr. În acest exemplu, numărul zecimal va avea un indice de 10, iar numărul binar va avea un indice de 2.

Pasul 2. Faceți împărțirea
Scrieți răspunsul întreg (coeficientul) sub simbolul divizării lungi și scrieți restul (0 sau 1) în dreapta numărului divizat.
Deoarece împărțim la doi, când numărul împărțit este un număr par, restul este 0, iar când numărul împărțit este un număr impar, restul este 1

Pasul 3. Continuați să împărțiți până ajunge la zero
Continuați în jos, împărțind fiecare nou cocient la doi și scriind restul în dreapta fiecărui număr împărțit. Opriți-vă când coeficientul este zero.

Pasul 4. Notați noul număr binar
Începând de la cel mai mic număr rămas, citiți ordinea restului în ordine crescătoare până sus. În acest exemplu, ar trebui să obțineți rezultatul 10011100. Acesta este echivalentul binar al numărului zecimal 156. Sau, dacă este scris cu indicele său de bază numerică: 15610 = 100111002.
Această metodă poate fi modificată pentru a converti de la baza zecimală la orice bază numerică. Divizorul este 2 deoarece baza sistemului numeric de destinație este baza 2 (binar). Dacă baza sistemului de numere de destinație este o altă bază, înlocuiți numărul de bază 2 din această metodă cu numărul de bază corespunzător. De exemplu, dacă baza de destinație este baza 9, înlocuiți numărul de bază 2 cu 9. Rezultatul final va fi direct sub forma numărului de bază de destinație
Metoda 2 din 2: Puterea de derivare a două și scăderea

Pasul 1. Începeți prin crearea unui tabel
Notați puterile celor două numere de bază în „baza tabelului 2” de la dreapta la stânga. Începeți de la 20, scrieți-l ca „1”. Ridicați rangul cu 1 pentru fiecare rang. Completați tabelul până când obțineți un număr care este cel mai apropiat de numărul sistemului zecimal pe care îl calculați. Pentru acest exemplu, să convertim numărul zecimal 15610 fie un număr binar.

Pasul 2. Găsiți numărul cu cea mai mare putere a numărului de bază 2
Din tabel, alegeți cel mai mare număr care este egal sau mai mic decât numărul care urmează să fie convertit. Numărul 128 este numărul cu cea mai mare putere a numărului de bază 2 și este, de asemenea, mai mic decât 156, deci scrieți un număr "1" sub această casetă din tabel, unde cel mai mare număr din tabel este în stânga (a se vedea tabelul în imaginea de mai sus). Apoi scădeți 128 din numărul inițial, veți obține: 156 - 128 = 28.
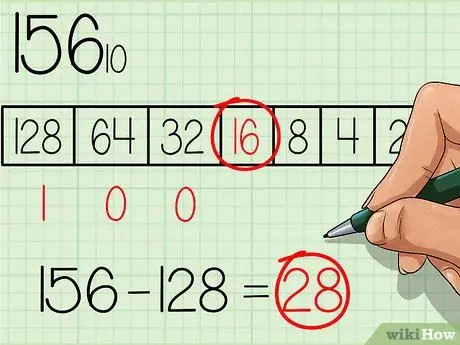
Pasul 3. Treceți la următoarea putere mai mică din tabel
Folosind noul număr (28), continuați prin tabel de la stânga la dreapta în timp ce verificați dacă numerele sunt egale sau mai mici decât noul număr. Numărul 64 nu este mai mic de 28, deci scrieți numărul „0” sub caseta numerică 64. Continuați până când găsiți un număr egal sau mai mic decât 28.
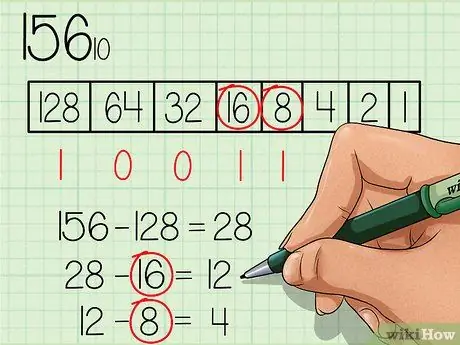
Pasul 4. Scadeți fiecare număr care este egal sau mai mic decât noul număr continuu și marcați numărul „1” sub casetă pentru numărul corespunzător
Numărul 16 este mai mic decât 28, deci scrieți numărul "1" sub caseta numerică 16 și scădeți 16 din 28, astfel încât să obțineți un nou număr 12. Numărul 8 este mai mic decât 12, deci scrieți numărul "1" sub caseta numerică 8 și scăderea 8 din 12 pentru a obține noul număr 4.

Pasul 5. Continuați până ajungeți la capătul mesei
Nu uitați să marcați un „1” sub fiecare casetă pentru numerele care sunt egale sau mai mici decât numărul nou și un „0” sub fiecare casetă pentru numerele care sunt încă mai mari decât numărul nou.
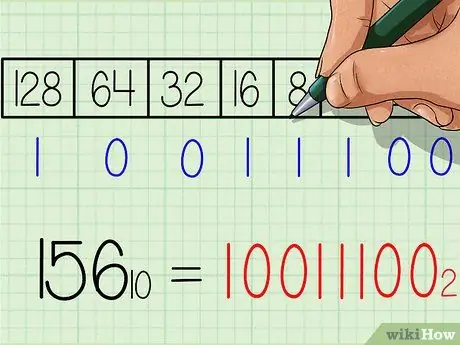
Pasul 6. Notați răspunsul pentru numărul binar
Numărul va fi exact același de la stânga la dreapta ca rândul numerelor „1” și „0” din partea de jos a tabelului. Ar trebui să obțineți rezultatul 10011100. Acesta este echivalentul binar al numărului zecimal 156. Sau atunci când este scris cu un indice: 15610 = 100111002.
Repetarea acestei metode vă poate ajuta să vă amintiți puterile bazei două, astfel încât să puteți sări peste pasul 1
sfaturi
- Programul Calculator încorporat în sistemul de operare poate face această conversie pentru dvs., dar în calitate de programator, cel mai bine este să începeți cu o bună înțelegere a modului în care funcționează conversiile. Opțiunile de conversie din programul Calculator pot fi făcute vizibile deschizând meniul „Vizualizare” și selectând „Programator” (pentru Windows 7 și 8).
- Conversia în direcția opusă, adică de la sistemul numeric binar la cel zecimal, este de obicei mai ușor de învățat mai întâi.
- Deseori practicați conversia numerelor zecimale în binare pentru a deveni mai experți.






