- Autor Jason Gerald [email protected].
- Public 2024-01-15 08:22.
- Modificat ultima dată 2025-01-23 12:43.
Gravitația este una dintre forțele fundamentale din fizică. Cel mai important aspect al gravitației este că este universal: toate obiectele au o forță gravitațională care atrage alte obiecte. Mărimea forței gravitaționale depinde de masă și de distanța dintre cele două obiecte.
Etapa
Partea 1 din 2: Calculul forței gravitației între două obiecte

Pasul 1. Definiți ecuația forței gravitaționale care trage un obiect, Fgrav = (Gm1m2) / d2.
Pentru a putea calcula forța gravitațională a unui obiect, această ecuație ia în considerare și masele celor două obiecte și distanța lor între ele. Variabilele ecuației sunt descrise mai jos.
- Fgrav este forța gravitațională
- G este constanta gravitațională universală 6,673 x 10-11 Nm2/kg2
- m1 este masa primului obiect
- m2 este masa celui de-al doilea obiect
- d este distanța dintre centrele celor două obiecte
- Uneori găsești litera r în loc de d. Aceste două simboluri reprezintă distanța dintre cele două obiecte.

Pasul 2. Folosiți unitățile metrice corespunzătoare
Pentru această ecuație, trebuie să utilizați unități metrice. Masa obiectului trebuie să fie în kilograme (kg), iar distanța dintre obiecte trebuie să fie în metri (m). Trebuie să convertiți aceste unități în unități metrice înainte de a continua

Pasul 3. Determinați masa obiectului în cauză
Pentru obiectele mici, le puteți cântări pentru a determina greutatea lor în kilograme. Pentru obiectele mari, puteți căuta masa aproximativă pe o masă sau pe internet. În problemele de fizică, de obicei se va spune masa obiectului.

Pasul 4. Măsurați distanța dintre cele două obiecte
Dacă încercați să calculați forța gravitațională dintre un obiect și pământ, trebuie să știți cât de departe este acest obiect de centrul pământului.
- Distanța de la suprafața pământului până la centrul pământului este de aproximativ 6,38 x 106 m.
- Puteți căuta tabele sau alte surse pe internet care vă spun distanța aproximativă de la centrul pământului la obiecte la diferite înălțimi de pe suprafața pământului.

Pasul 5. Finalizați calculul
Dacă ați definit variabilele din ecuație, nu ezitați să le introduceți pentru a le rezolva. Asigurați-vă că toate variabilele sunt în unități metrice și sunt scalate corespunzător. Masa trebuie să fie în kilograme și distanța trebuie să fie în metri. Rezolvați ecuațiile în ordinea corectă a calculelor.
- De exemplu, determinați forța gravitațională a unei persoane a cărei masă este de 68 kg deasupra suprafeței pământului. Masa Pământului este de 5,98 x 1024 kg.
- Asigurați-vă că toate variabilele sunt în unități corecte. m1 = 5, 98 x 1024 kg, m2 = 68 kg, G = 6,673 x 10-11 Nm2/kg2și d = 6, 38 x 106 m
- Scrieți ecuația: Fgrav = (Gm1m2) / d2 = [(6, 67 x 10-11) x 68 x (5, 98 x 1024)] / (6, 38 x 106)2
- Înmulțiți masele celor două obiecte care sunt luate în considerare. 68 x (5, 98 x 1024) = 4,06 x 1026
- Înmulțiți rezultatul m1 si m2 cu constanta gravitațională G. (4,06 x 1026) x (6,67 x 10-11) = 2.708 x 1016
- Păstrați distanța dintre cele două obiecte. (6, 38 x 106)2 = 4,07 x 1013
- Împărțiți rezultatul G x m1 x m2 după distanța pătrată pentru a obține forța gravitațională în Newtoni (N). 2, 708 x 1016/ 4, 07 x 1013 = 665 N
- Forța sa gravitațională este de 665 N.
Partea 2 din 2: Calculul Forței Gravitației pe Pământ

Pasul 1. Înțelegeți a doua lege a lui Newton, F = ma
A doua lege a lui Newton afirmă că accelerația unui obiect este direct proporțională cu forța netă care acționează asupra acestuia și invers proporțională cu masa acestuia. Cu alte cuvinte, dacă o forță care acționează asupra unui obiect este mai mare decât forța care acționează în direcția opusă, obiectul se va deplasa cu forța mai puternică.
- Această lege poate fi rezumată prin ecuația F = ma, unde F este forța, m este masa obiectului și a este accelerația.
- Datorită acestei legi, putem calcula forța gravitațională a tuturor obiectelor de pe suprafața pământului, folosind accelerația cunoscută datorată gravitației.
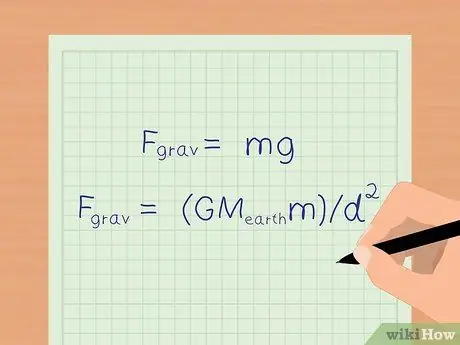
Pasul 2. Găsiți accelerația datorată gravitației Pământului
Pe pământ, forța gravitațională determină accelerarea tuturor obiectelor cu 9,8 m / s2. La suprafața pământului, putem folosi o ecuație simplificată: Fgrav = mg pentru a calcula forța gravitațională.
Dacă doriți să cunoașteți un număr mai precis de forțe gravitaționale, puteți utiliza în continuare formula din pasul anterior, Fgrav = (GMPământm) / d2 pentru a determina forța gravitațională.

Pasul 3. Folosiți unitățile metrice corespunzătoare
Pentru această ecuație, trebuie să utilizați unități metrice. Masa obiectului trebuie să fie în kilograme (kg), iar distanța dintre obiecte trebuie să fie în metri (m). Trebuie să convertiți aceste unități în unități metrice înainte de a continua.

Pasul 4. Determinați masa obiectului în cauză
Pentru obiectele mici, le puteți cântări pentru a determina greutatea lor în kilograme. Pentru obiectele mari, puteți căuta masa aproximativă pe o masă sau pe internet. În problemele de fizică, de obicei se va spune masa obiectului.

Pasul 5. Finalizați calculul
Dacă ați definit variabilele din ecuație, nu ezitați să le introduceți pentru a le rezolva. Asigurați-vă că toate variabilele sunt în unități metrice și sunt scalate corespunzător. Masa trebuie să fie în kilograme și distanța trebuie să fie în metri. Rezolvați ecuațiile în ordinea corectă a calculelor.
- Să încercăm să folosim ecuația din pasul anterior și să vedem cât de apropiate sunt rezultatele. Determinați forța gravitațională a unei persoane cu o masă de 68 kg pe suprafața pământului.
- Asigurați-vă că toate variabilele sunt în unități corecte: m = 68 kg, g = 9,8 m / s2.
- Notați formula. Fgrav = mg = 68 * 9, 8 = 666 N.
- Folosind formula F = mg forța gravitațională este de 666 N, în timp ce rezultatul din formula din pasul anterior este de 665 N. După cum puteți vedea, cele două rezultate sunt aproape aceleași.
sfaturi
- Aceste două formule ar trebui să dea același răspuns, dar formula mai scurtă și mai simplă este mai ușor de utilizat atunci când se discută despre obiecte de pe suprafața unei planete.
- Folosiți prima formulă dacă nu cunoașteți accelerația datorată gravitației pe o planetă sau calculați forța gravitațională dintre două obiecte foarte mari, cum ar fi luna sau planetele.






