Reciprocul sau reciprocul este foarte util în toate tipurile de ecuații algebrice. De exemplu, atunci când împărțiți o fracție la alta, înmulțiți prima fracție cu reciprocul celei de-a doua. De asemenea, trebuie să utilizați inversul atunci când căutați ecuația unei linii.
Etapa
Metoda 1 din 3: Găsirea inversului unei fracții sau a unui întreg
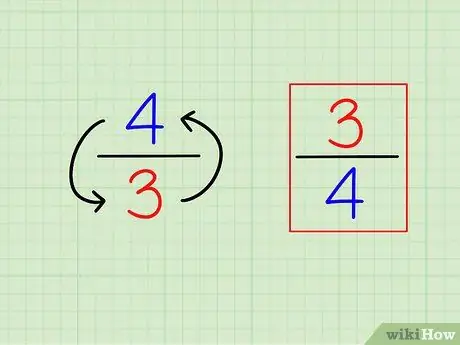
Pasul 1. Găsiți reciprocul fracției inversând-o
Definiția „reciproc” sau opusul este foarte ușoară. Pentru a găsi reciprocitatea oricărui număr întreg, calculați pur și simplu „1 (acel număr)”. Pentru fracții, reciprocul este o fracție diferită, adică numerele sunt „inversate” (invers).
- De exemplu, opusul lui 3/4 este 4/3.
- Orice număr înmulțit cu randamentele sale reciproce 1.
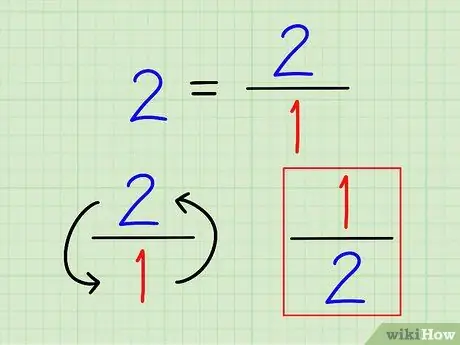
Pasul 2. Scrieți reciprocul numărului întreg ca o fracție
Din nou, reciprocitatea unui număr este întotdeauna 1 (acel număr). Pentru numere întregi, scrieți-le ca fracții. Nu are rost să calculăm acel număr cu o zecimală.
De exemplu, reciprocitatea lui 2 este 1 2 = 1/2.
Metoda 2 din 3: Găsirea inversă a unei fracții mixte
Pasul 1. Identificați numerele mixte
Fracțiile mixte constau din numere întregi și fracții, cum ar fi 24/5. Există doi pași pentru a găsi reciprocul unui număr mixt, așa cum este descris mai jos.
Pasul 2. Conversia numerelor mixte în fracții necorespunzătoare
Amintiți-vă că 1 poate fi întotdeauna scris ca (număr) / (același număr), iar fracțiile cu același numitor (numărul de jos) pot fi adăugate împreună. Iată un exemplu folosind 24/5:
- 24/5
- = 1 + 1 + 4/5
- = 5/5 + 5/5 + 4/5
- = (5+5+4)/5
- = 14/5.
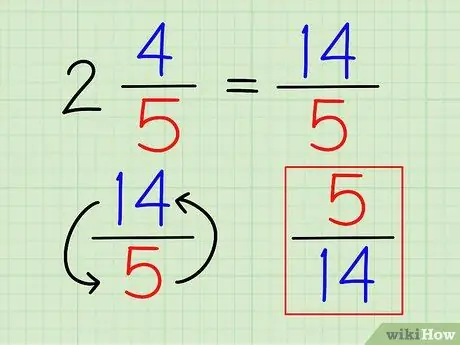
Pasul 3. Întoarceți fracția
Odată ce numărul este scris complet ca o fracție, puteți găsi reciprocul său la fel ca orice altă fracție, inversând fracția.
În exemplul de mai sus, reciprocitatea lui 14/5 este 5/14.
Metoda 3 din 3: Găsirea opusului unei zecimale
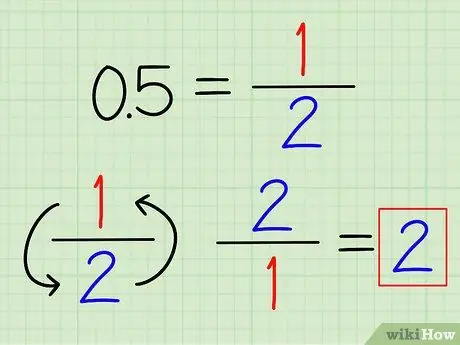
Pasul 1. Convertește zecimale în fracții, dacă este posibil
Puteți recunoaște unele numere zecimale utilizate frecvent, care pot fi ușor convertite în fracții. De exemplu, 0,5 = 1/2 și 0,25 = 1/4. Odată ce zecimalul a fost convertit într-o fracție, pur și simplu răsturnați fracția pentru a-i găsi reciprocitatea.
De exemplu, reciprocitatea de 0,5 este 2/1 = 2.
Pasul 2. Scrieți o problemă de divizare
Dacă nu îl puteți converti într-o fracție, calculați reciprocul numărului sub forma unei probleme de divizare: 1 (zecimal). Puteți utiliza un calculator pentru a-l rezolva sau puteți trece la pasul următor pentru a-l rezolva manual.
De exemplu, puteți găsi reciprocul de 0,4 calculând 1 0,4
Pasul 3. Schimbați problema divizării pentru a utiliza numerele întregi
Primul pas pentru împărțirea zecimalelor este mutarea punctului zecimal până când toate numerele sunt numere întregi. Atâta timp cât mutați punctul zecimal al ambelor numere cu același număr de pași, veți obține răspunsul corect.
De exemplu, puteți utiliza 1 0, 4 și rescrie-l ca 10 4. În acest caz, mutați toate zecimalele cu un pas spre dreapta, în același mod în care înmulțiți fiecare număr cu zece
Pasul 4. Rezolvați problema folosind împărțirea lungă
Utilizați metoda divizării lungi pentru a calcula reciprocul. Dacă numărați 10 4, veți primi răspunsul 2, 5 care este reciprocul lui 0, 4.
sfaturi
- Reciprocul negativ al unui număr este același cu reciprocul regulat, în sensul că este înmulțit cu unul negativ. De exemplu, reciprocitatea negativă a 3/4 este -4/3.
- Reciprocul sau reciprocul este adesea denumit „inversarea multiplicării”.
- Numărul 1 este opusul său, deoarece 1 1 = 1.
- Numărul 0 nu are reciproc, deoarece 0 este nedefinit.
