În statistici, intervalul este diferența dintre cea mai mare valoare dintr-un set de date și cea mai mică valoare dintr-un set de date. Gama arată cât de răspândite sunt valorile într-o serie. Dacă gama este un număr mare, atunci valorile din serie sunt foarte dispersate; dacă intervalul este un număr mic, atunci valorile din serie sunt apropiate unele de altele. Dacă doriți să știți cum să calculați acoperirea, urmați acești pași.
Etapa
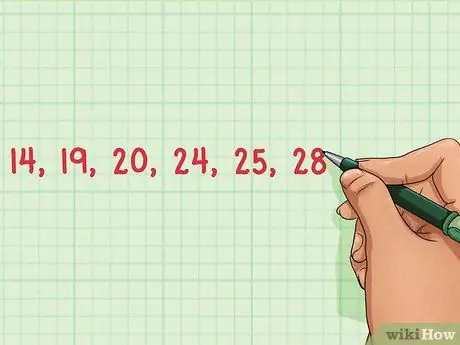
Pasul 1. Enumerați elementele setului de date
Pentru a găsi intervalul unui set de date, trebuie să enumerați toate elementele din setul de date, astfel încât să puteți identifica cele mai mari și cele mai mici numere. Notați toate elementele. Numerele din acest set de date sunt: 14, 19, 20, 24, 25 și 28.
- Este mai ușor să identificați cele mai mari și cele mai mici numere dintr-un set de date dacă comandați numerele de la cel mai mic la cel mai mare. În acest exemplu, setul de date ar fi structurat astfel: 14, 19, 20, 24, 24, 25, 28.
- Sortarea elementelor într-un set de date vă va ajuta, de asemenea, să efectuați alte calcule, cum ar fi găsirea modului, a mediei sau a medianei setului de date.
Pasul 2. Identificați cele mai mari și cele mai mici numere din setul de date
În această problemă, cel mai mic număr din setul de date este 14 și cel mai mare număr este 28.
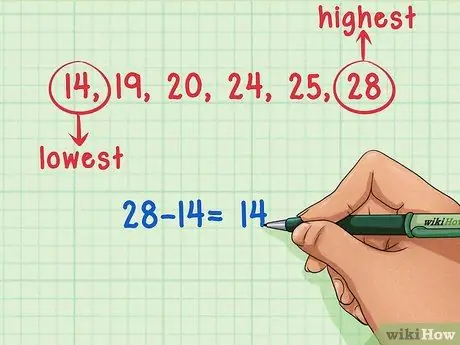
Pasul 3. Scădeți cel mai mic număr din setul de date din cel mai mare număr
Acum că ați identificat cele mai mici și mai mari numere din setul de date, tot ce trebuie să faceți este să le scădeți unul de celălalt. Scădeți 14 din 25 (25 - 14) pentru a obține 11, intervalul setului de date.
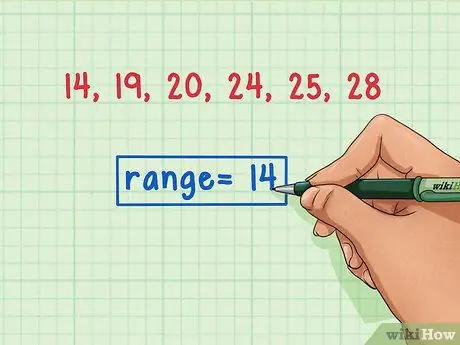
Pasul 4. Etichetați clar gama
După ce găsiți gama, etichetați-o clar. Acest lucru vă va ajuta să evitați confuzia cu alte calcule statistice pe care trebuie să le efectuați, cum ar fi găsirea medianei, modului sau mediei.
sfaturi
- De asemenea, puteți interpreta intervalul în termeni algebrici, dar trebuie mai întâi să înțelegeți conceptul unei funcții algebrice sau un set de operații pe numere cunoscute. Deoarece operațiile funcționale pot fi efectuate pe orice număr, chiar și pe un număr necunoscut, numărul este notat printr-o variabilă literă, de obicei x. Un domeniu este un set de valori de intrare posibile, pe care le puteți înlocui cu numărul necunoscut. Astfel, intervalul este setul posibilelor rezultate de calcul, pe care le obțineți după introducerea uneia dintre valorile domeniului și finalizarea tuturor operațiunilor definite de funcție. Din păcate, nu există nicio modalitate de a calcula intervalul unei funcții. Uneori, graficarea unei funcții sau calcularea mai multor valori poate arăta un model clar. De asemenea, vă puteți folosi cunoștințele despre domeniul funcției pentru a renunța la valorile posibile de ieșire (rezultate de calcul) sau pentru a restrânge setul de date care reprezintă intervalul.
- Valoarea mediană a oricărui set de date statistice reprezintă valoarea mediană a setului de date în ceea ce privește distribuția datelor, nu intervalul. Deci, deși poate doriți să presupuneți că mediana unui anumit set de date este intervalul împărțit la 2 - sau jumătate din intervalul - acest lucru nu este de obicei adevărat. Pentru a găsi mediana corectă, trebuie să sortați elementele de date, apoi să căutați elementul din mijlocul listei. Acest element este mediana. De exemplu, dacă aveți o listă de 29 de elemente, cel de-al 15-lea element are același interval de la începutul listei și la sfârșitul listei, deci cel de-al 15-lea element este mediana, indiferent de modul în care se referă valoarea acelui element gama.
