- Autor Jason Gerald [email protected].
- Public 2024-01-15 08:22.
- Modificat ultima dată 2025-01-23 12:43.
S-ar putea să credeți că numerele întregi sunt doar numere obișnuite, cum ar fi 3, -12, 17, 0, 7000 sau -582. Numerele întregi sunt, de asemenea, numite numere întregi, deoarece nu sunt împărțite în părți precum fracții și zecimale. Citiți acest articol pentru a afla tot ce aveți nevoie despre adăugarea și scăderea de numere întregi sau citiți direct secțiunea de care aveți nevoie.
Etapa
Metoda 1 din 5: Adunarea și scăderea numerelor întregi pozitive folosind o linie numerică

Pasul 1. Înțelegeți linia numerică
Liniile numerice transformă matematica de bază în ceva tangibil și fizic pe care îl puteți vedea. Cu doar câteva semne și bun simț, îl putem folosi ca un calculator pentru a aduna și scădea numere.

Pasul 2. Desenați o linie numerică de bază
Imaginați-vă sau trasați o linie dreaptă uniformă. Faceți un punct în mijlocul liniei. Scrie 0 sau zero lângă această perioadă.
Cartea dvs. de matematică ar putea numi acest punct de plecare, deoarece este punctul de plecare pentru toate numerele

Pasul 3. Desenați două puncte, fiecare la dreapta și la stânga zero
Scrie - 1 lângă punctul din stânga și
Pasul 1. lângă punctul din dreapta. Acesta este întregul cel mai apropiat de zero.
- Nu vă faceți griji dacă faceți distanțele dintre puncte exact la fel - atâta timp cât știți ce înseamnă fiecare punct, poate fi utilizată o linie numerică.
- Partea stângă este începutul propoziției.

Pasul 4. Completați linia numerică adăugând mai multe numere
Faceți mai multe puncte la stânga decât -1 și la dreapta decât 1. În stânga, de la -1, marcați punctele cu - 2, - 3, și - 4. În dreapta, de la 1, marcați-vă punctul cu
Pasul 2
Pasul 3., da
Pasul 4.. Puteți continua dacă aveți spațiu pe hârtie.
Exemplul din figură arată o linie numerică de la -6 la 6

Pasul 5. Înțelegeți despre numerele întregi pozitive și negative
Numere întregi pozitive, numite și numar natural, este un număr întreg mai mare decât zero. 1, 2, 3, 25, 99 și 2007 sunt numere întregi pozitive. Numere întregi negative sunt numere întregi mai mici de zero (cum ar fi -2, -4 și -88).
Numerele întregi sunt un alt mod de a apela numerele întregi. Fracțiile precum 1/2 (jumătate) sunt doar o parte din număr, deci nu sunt numere întregi. La fel ca zecimal, de exemplu 0,25 (punctul zero doi cinci); zecimal nu este un număr întreg

Pasul 6. Începeți să rezolvați 1 + 2 plasând degetul pe punctul 1
Vom rezolva probleme simple de adăugare 1+2 folosind linia numerică pe care tocmai ați creat-o. Primul număr este
Pasul 1., așa că începeți să puneți degetul pe număr.
-
Este prea ușoară această întrebare?
Dacă ați adăugat vreodată, probabil că știți răspunsul la 1 + 2. Bine: dacă cunoașteți rezultatul, va fi mai ușor să înțelegeți cum funcționează linia numerică. Apoi, puteți utiliza linia numerică pentru a rezolva probleme de adunare mai dificile sau pentru a vă pregăti pentru matematici mai dificile, cum ar fi algebra.

Pasul 7. Adăugați 1 + 2 mișcând degetul 2 puncte spre dreapta
Glisați degetul spre dreapta, numărând numărul de puncte (un alt număr) pe care îl treceți. Dacă ai trecut de 2 puncte noi, oprește-te. Numărul pe care îl arată degetul este răspunsul,
Pasul 3
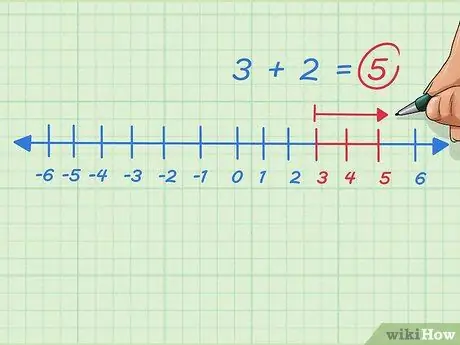
Pasul 8. Adăugați orice număr întreg pozitiv deplasându-vă la dreapta pe linia numerică
Să presupunem că vrem să rezolvăm 3 + 2. Începeți de la 3, mutați-vă la dreapta sau adăugați 2 puncte. Ne oprim la 5. Problema este scrisă 3 + 2 = 5.

Pasul 9. Se scade numere întregi pozitive deplasându-se la stânga pe linia numerică
De exemplu, vrem să rezolvăm 6-4, începem de la 6, ne deplasăm la stânga cu 4 puncte și ne oprim la 2. Această problemă este scrisă 6 - 4 = 2.
Metoda 2 din 5: Adunarea și scăderea numerelor negative folosind o linie numerică

Pasul 1. Aflați despre liniile numerice
Dacă nu știți cum să creați o linie numerică, reveniți la secțiunea Adăugarea și scăderea numerelor pozitive folosind linii numerice pentru a afla cum să creați una.
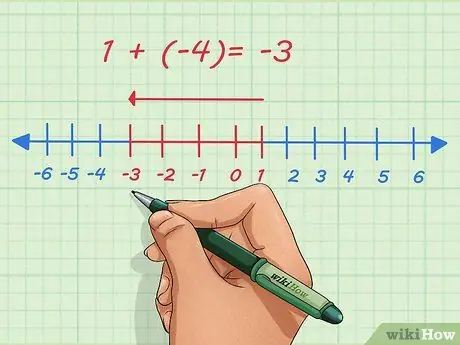
Pasul 2. Înțelegeți despre numerele negative
Numerele pozitive sunt indicate de direcția din dreapta pe linia numerică. Numerele negative sunt indicate în stânga pe linia numerică. Adăugarea numerelor negative înseamnă deplasarea punctului spre stânga pe linia numerică.
-
De exemplu, să adăugăm 1 și -4. De obicei, această întrebare este scrisă astfel:
1 + (-4)
. Pe linia numerică, începem de la 1, mutăm 4 puncte spre stânga și ne oprim la -3.
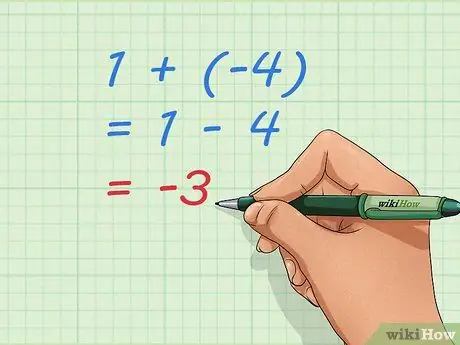
Pasul 3. Folosiți ecuațiile de bază pentru a înțelege adunarea numerelor negative
Observați că -3, răspunsul nostru, este numărul pe care îl vom obține dacă facem 1 - 4. Adunarea 1 + (-4) și scăderea 4 din 1 este aceeași problemă. O putem scrie ca o ecuație, o propoziție matematică care arată egalitate: 1 + (-4) = 1 - 4 = -3
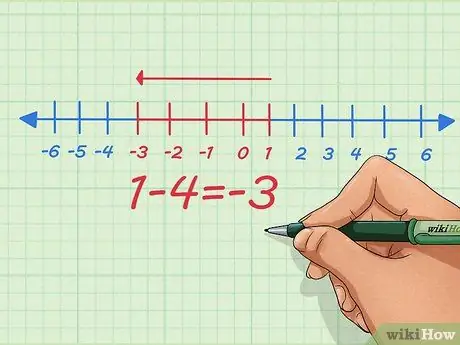
Pasul 4. În loc să adăugați numere negative, transformați-l într-o problemă de scădere folosind numere pozitive
După cum putem vedea din ecuația simplă de mai sus, putem face ambele - transformăm adunarea numerelor negative în scăderea numerelor pozitive și invers. Este posibil să fi fost învățat să transforme negativele în negative fără să știi de ce - iată de ce.
-
De exemplu, -4. Când adunăm -4 și 1, scădem 1 cu 4. Poate fi scris în matematică prin scriere
1 + (-4) = 1 - 4
. Putem scrie acest lucru pe linia numerică, începând de la punctul nostru de pornire la 1, apoi adăugând 4 puncte la stânga (cu alte cuvinte, adăugând -4). Deoarece aceasta este o ecuație, un lucru este egal cu altul - deci este adevărat și opusul
1 - 4 = 1 + (-4)
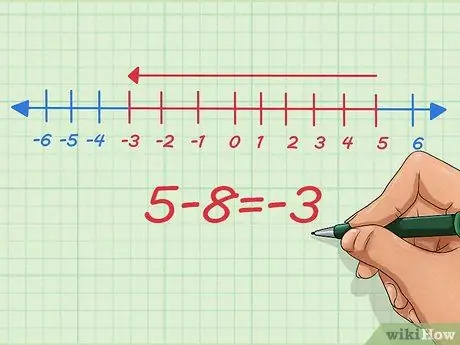
Pasul 5. Înțelegeți cum puteți scădea numerele negative pe o linie numerică
Pe linia numerică, scăderea numerelor negative este aceeași cu reducerea lungimii. Să începem cu 5 - 8.
Pe linia numerică, începem de la punctul nostru de pornire la 5, scădem 8 și ne oprim la -3
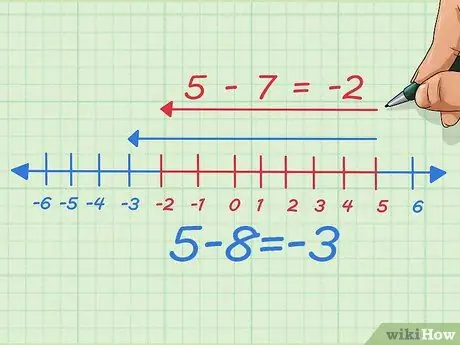
Pasul 6. Scade suma pe care o scazi și vezi ce se întâmplă
Să presupunem că scădem unul, numărul pe care îl scădem sau, cu alte cuvinte, scădem 7 în loc de 8. Acum scădem un punct la stânga pe linia numerică. În scris, am început cu 5 - 8 = -3 Acum, mutăm doar 7 la stânga, deci devine 5 - 7 = -2
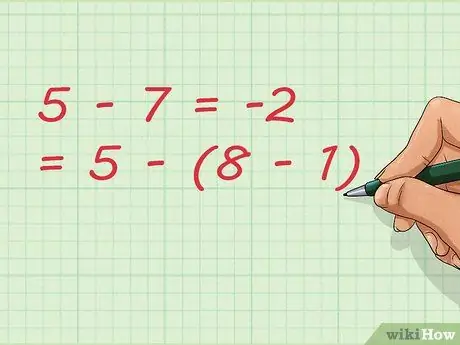
Pasul 7. Observați că scăderea poate rezulta în plus
În exemplul nostru, scădem numărul 1. În scrierea ecuației, o putem scrie mai scurt ca: 5 - 7 = -2 = 5 - (8 - 1)

Pasul 8. Convertiți semnele negative în pozitive atunci când adăugați numere negative
Folosind pasul de conversie a tuturor scăderilor în adunări, putem scrie altele mai scurte precum: 5 - (8 - 1) = 5 - 7 = 5 - 8 + 1.
-
Știm deja că 5 - 8 = -3, deci scoateți 5 - 8 din ecuație și introduceți -3:
5 - (8 - 1) = 5 - 7 = -3 + 1
-
Știm deja că 5 - (8 - 1) este - scade un punct din 5 - 8. Ecuația noastră poate arăta că 5 - 8 este egal cu -3, iar scăderea unui punct dă -2. Ecuația poate fi scrisă astfel:
-3 - (-1) = -3 + 1
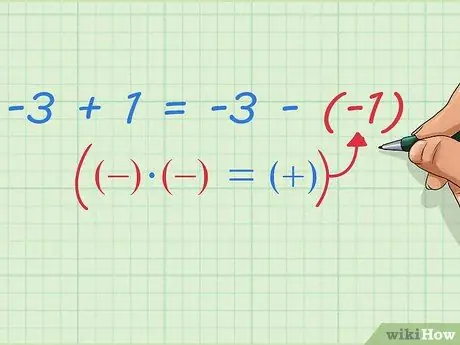
Pasul 9. Scrieți scăderea numerelor negative ca adunare
Observați ce se întâmplă după aceasta - am dovedit deja că: -3 + 1 = -3 - (-1) Putem scrie acest lucru cu reguli de scriere matematică mai simple și mai generale: primul număr plus al doilea număr = primul număr minus (al doilea număr negativ) Sau, un mod mai simplu pe care l-ați auzit probabil la ora de matematică: Schimbați cele două semne negative într-un semn pozitiv.
Metoda 3 din 5: Adăugarea unor numere întregi mari pozitive

Pasul 1. Scrieți problema adunării de 2.503 + 7.461 cu un număr peste celălalt
Notați numerele în coloana mare astfel încât 2 să fie peste 7, 5 să fie peste 4 și așa mai departe. În acest fel, vom învăța cum să adăugăm numere întregi care sunt prea mari pentru a ne imagina sau utiliza linia numerică.
Scrieți un semn + în stânga numărului de mai jos și linia de sub acesta, pentru că ați putea învăța pentru probleme de adăugare mai mici
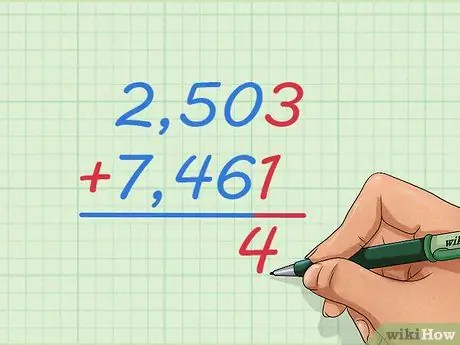
Pasul 2. Începeți prin adunarea celor două numere din extrema dreaptă
Ar putea fi puțin ciudat să începem de la dreapta, deoarece citim numere din stânga. Trebuie să adăugăm din dreapta pentru a obține răspunsul corect, pe care îl puteți vedea mai târziu.
-
Sub cele două numere din dreapta,
Pasul 3. da
Pasul 1., scrieți suma celor două
Pasul 4..

Pasul 3. Adăugați fiecare număr din coloană în același mod
Deplasați-vă spre stânga, adăugați 0+6, 5+4, și 2+7. Scrieți răspunsul sub fiecare pereche de numere.
Răspunsul dvs. ar trebui să fie: 9.964. Verifică-ți munca dacă greșești.

Pasul 4. Acum adăugați 857 + 135
Veți observa ceva diferit imediat ce adăugați prima pereche de numere din dreapta. 7+5 este egal cu 12, un număr din două cifre, dar nu puteți scrie decât o cifră sub coloana respectivă. Continuați să citiți pentru a afla ce ar trebui să faceți și de ce ar trebui să începeți întotdeauna de la dreapta și nu de la stânga.

Pasul 5. Adăugați 7 + 5 și aflați unde să scrieți răspunsul
7 + 5 = 12, dar nu puteți pune 1 și 2 sub linie. Dar, scrieți ultima cifră, Pasul 2., sub linie și notați prima cifră
Pasul 1., deasupra coloanei din stânga, 5 + 3.
-
Dacă sunteți curios cu privire la modul în care funcționează, gândiți-vă la ce înseamnă împărțirea 1 și 2. De fapt, împărțiți 12 în
Pasul 10. da
Pasul 2.. Puteți scrie 10 deasupra numărului dacă doriți și veți vedea 1 în coloanele 5 și 3, la fel ca înainte.

Pasul 6. Adăugați 1 + 5 + 3 pentru a obține următoarea cifră a răspunsului
Acum aveți trei cifre de adăugat, deoarece ați adăugat 1 la această coloană. Raspunsul este
Pasul 9., deci răspunsul tău devine 92.
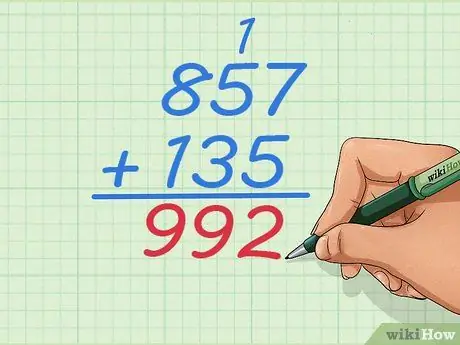
Pasul 7. Completați problema ca de obicei
Continuați să lucrați cifrele din stânga până când ați adăugat toate numerele, în acest caz, a mai rămas o singură coloană. Răspunsul dvs. final ar trebui să fie 992.
- Puteți încerca întrebări mai complicate, cum ar fi 974 + 568. Amintiți-vă, ori de câte ori obțineți un număr din două cifre, scrieți ultima cifră doar ca răspuns și plasați cealaltă cifră deasupra coloanei din stânga, pe care o veți adăuga în continuare. Dacă răspunsul din ultima coloană (în stânga) conține două cifre, scrieți-l ca răspuns.
- Consultați secțiunea Sfaturi pentru răspunsuri la întrebările 974 + 568 după ce ați încercat să le rezolvați.
Metoda 4 din 5: scăderea numerelor întregi pozitive mari

Pasul 1. Scrieți problema scăderii 4.713 - 502 cu primul număr deasupra celui de-al doilea număr
Scrieți-l astfel încât 3 să fie direct peste 2, 1 să fie peste 0, 7 să fie peste 5 și 4 să fie deasupra golului.
Puteți scrie 0 sub 4 dacă acest lucru vă ajută să vă amintiți care număr este peste care număr. Puteți adăuga oricând un 0 în fața unui număr fără a-l modifica. Asigurați-vă că îl adăugați înainte de număr, nu după acesta

Pasul 2. Se scade fiecare număr de mai jos din numărul de deasupra acestuia
Începeți întotdeauna de la dreapta. Rezolvați 3-2, 1-0, 7-5 și 4-0, scrieți răspunsul la fiecare întrebare direct sub cele două numere scăzute.
Rezultatul este, 4.211.

Pasul 3. Acum scrieți întrebările 924 - 518 în același mod
Aceste numere au același număr de cifre, astfel încât să le puteți nota cu ușurință. Această problemă vă va învăța ceva despre scăderea numerelor întregi dacă nu o știți deja.

Pasul 4. Aflați cum să rezolvați prima problemă, care se află în extrema dreaptă
4 - 8. Această problemă este complicată deoarece 4 este mai mică de 8, dar nu utilizați numere negative, dar urmați acești pași:
- În rândul de sus, încrucișați 2 și scrieți 1. 2 trebuie să fie în stânga lui 4.
- Cruceați 4 și scrieți 14. Faceți acest lucru într-un spațiu îngust, astfel încât să fie clar că 14 depășește 8. De asemenea, puteți scrie 1 în fața lui 4 pentru a face 14 dacă există suficient spațiu.
- Ceea ce tocmai ați făcut este să împrumutați 1 din locul zecilor sau a doua coloană din dreapta și convertiți-l la 10 în locul celor sau coloana din dreapta. Odată ce numărul 10 este egal cu de zece ori numărul 1, deci este la fel.

Pasul 5. Acum rezolvați problemele 14 - 8 și scrieți răspunsul în coloana din dreapta
Ar fi trebuit să scrie 6 pe linia de răspuns din dreapta.

Pasul 6. Completați următoarea coloană din stânga, folosind noul număr pe care l-ați notat
Scăderea ar trebui să fie 1 - 1, care este egal cu 0.
Răspunsul dvs. ar trebui să fie acum 06.

Pasul 7. Rezolvați problema completând ultima scădere, coloana din stânga
9 - 5 = 4, deci răspunsul dvs. final este 406.

Pasul 8. Acum rezolvăm problema scăderii numerelor mari din numere mici
Să presupunem că vi se cere să completați 415.990 - 968.772. Scrie al doilea număr sub primul număr și vei realiza că numărul de mai jos este mai mare! Puteți spune imediat din prima cifră din stânga: 9 este mai mare decât 4, deci numerele care încep cu 9 sunt mai mari.
Asigurați-vă că notați corect coloana înainte de a compara. 912 Nu mai mare de 5000 vă puteți da seama dacă scrieți corect coloana, deoarece nu există numere sub 5. Puteți adăuga zero ajutor, de exemplu, scrieți 912 cu 0912 astfel încât coloana să fie egală cu 5000.

Pasul 9. Scrieți numărul mai mic sub numărul mai mare și adăugați un semn - în fața răspunsului
Ori de câte ori scădeți un număr dintr-un număr mai mic, rezultatul este un număr negativ. Este mai bine să scrieți acest semn înainte de a scădea, astfel încât să nu uitați să-l scrieți.

Pasul 10. Pentru a răspunde, scădeți numărul mic din numărul mare și nu uitați să scrieți semnul -
Răspunsul dvs. va fi negativ, ceea ce este indicat printr-un semn -. Nu face încearcă să scadă un număr mare dintr-un număr mic, apoi face rezultatul negativ; răspunsul tău va fi greșit.
Noua problemă de rezolvat este: 968.772 - 415.990 = -? Consultați secțiunea Sfaturi pentru răspuns după ce ați încercat să rezolvați această problemă
Metoda 5 din 5: Adunarea și scăderea numerelor întregi negative
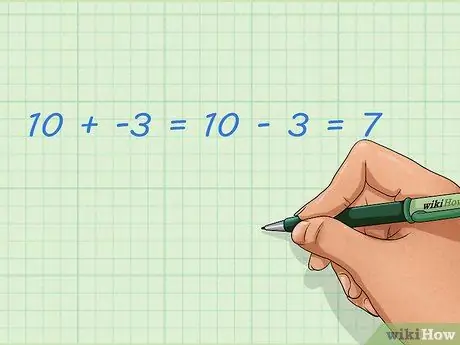
Pasul 1. Aflați cum să adăugați numere negative și pozitive
Adăugarea de numere întregi negative este la fel ca scăderea unor numere întregi pozitive. Acest lucru este mai ușor de făcut cu linia numerică descrisă în altă secțiune, dar vă puteți gândi și la cuvinte. Numerele negative nu sunt numere obișnuite; acest număr este mai mic decât zero și poate reprezenta suma luată. Dacă adăugați această preluare la un număr obișnuit, rezultatul devine mai mic.
- Exemplu: 10 + -3 = 10 - 3 = 7
- Exemplu: -12 + 18 = 18 + -12 = 18 - 12 = 6. Amintiți-vă că puteți schimba întotdeauna ordinea numerelor în plus, dar nu și prin scădere.
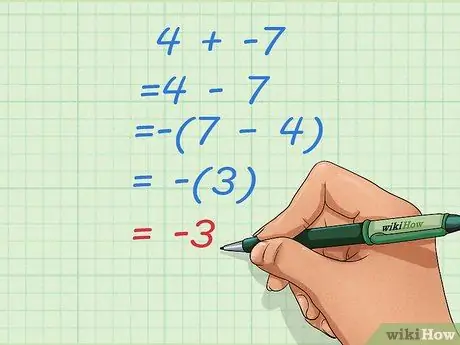
Pasul 2. Aflați ce trebuie să faceți dacă îl transformați într-o problemă de scădere cu un număr de pornire mai mic
Uneori, schimbarea adăugării la probleme de scădere, precum cea de mai sus, poate duce la răspunsuri ciudate, cum ar fi 4 - 7. Când se întâmplă acest lucru, inversați ordinea numerelor și faceți rezultatul negativ.
- Să presupunem că problema dvs. inițială este 4 + -7.
- Transformă-l într-o problemă de scădere: 4 - 7
- Inversați ordinea și faceți rezultatul negativ: - (7 - 4) = - (3) = -3.
- Dacă nu sunteți familiarizați cu utilizarea parantezelor în ecuații, gândiți-vă la acest lucru: 4 - 7 se transformă în 7 - 4 cu adăugarea unui semn negativ. 7 - 4 = 3, dar trebuie să-l schimbăm în -3, astfel încât răspunsul la întrebările 4 - 7 să fie corect.
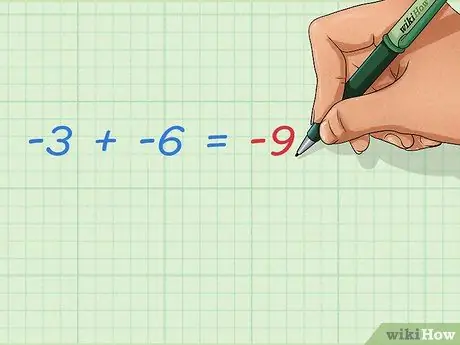
Pasul 3. Aflați cum să adăugați două numere întregi negative
Două numere negative adăugate fac întotdeauna rezultatul negativ mai mare. Deoarece nu se adaugă numere pozitive, rezultatul va fi mai departe de 0. Răspunsul este ușor:
- -3 + -6 = -9
- -15 + -5 = -20
- Vedeți tiparul? Tot ce trebuie să faceți este să adunați numerele ca și cum ar fi numere pozitive și adăugați un semn negativ. -4 + -3 = - (4 + 3) = -7
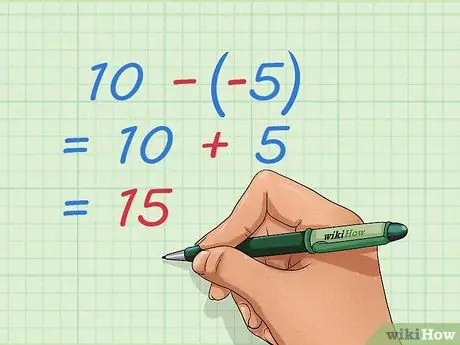
Pasul 4. Aflați cum puteți scădea numere întregi negative
La fel ca problema adăugării, puteți rescrie problema astfel încât să aveți doar numere pozitive. Dacă scădeți numere negative, eliminați unele dintre lucrurile care au fost deja luate, ceea ce înseamnă că adăugați numere pozitive.
- Gândiți-vă la numerele negative ca la bani furați. Dacă scădeți sau scoateți bani furați pentru a-i putea returna, este ca și cum ați da bani cuiva, nu?
- Exemplu: 10 - -5 = 10 + 5 = 15
- Exemplu: -1 - -2 = -1 + 2. Ai învățat deja cum să rezolvi această problemă în primul pas, îți amintești? Citiți din nou cum să adăugați numere negative și pozitive dacă ați uitat.
- Iată soluția completă a ultimului exemplu: -1 - -2 = -1 + 2 = 2 + -1 = 2 - 1 = 1.
sfaturi
- Este posibil să fi scris numere lungi precum 2.521.301 folosind virgule (,) în loc de (.) În funcție de locul în care locuiți. Folosiți ceea ce vă cere profesorul dvs. pentru a nu vă confunda cu alte sisteme de scriere.
- Desenează-ți liniile numerice pe diferite scale pentru a reprezenta numere diferite. Nu există nici o regulă conform căreia fiecare distanță pe o linie numerică este egală cu 1. Imaginați-vă o linie numerică care este 10 în loc de 1. În afară de faptul că fiecare punct este 10 acum, adunarea și scăderea rămân aceleași. Încercați dacă nu credeți.
- Dacă încercați întrebările speciale de provocare din secțiunea Numere lungi, iată răspunsul: 974 + 568 = 1.542. Răspunsul de la 415.990 - 968.772 este - 552.782.






